| BASE | HAUTEUR | OBSERVATIONS |
| 440 /11= 40 40 / 22 = 1,818181 Résultat irrationnel dans la géométrie de π. |
280 / 2 = 140 140 / 7 = 20 x 0,5238095 20 / 11 = 1,818181 |
Le nombre de coudées royales dénombrées dans les proportions de la pyramide de Khéops est fondé sur la fraction de 10, qui facilite le calcul, mais ne permet pas d’expliquer la valeur de π dans le tracé du cercle complet tel que représenté par les dessins 11 et 12. De même, la géométrie qui détermine les valeurs du périmètre du cercle n’a de réalité que par les nombres 7 et 11 que la fraction au dénominateur de 440 et 280 ne permet pas de rédiviser en des proportions plus petites qui restent rationnelles dans la valeur de π. Malgré sa périodicité, l’unité de 1,818181 ne permet aucune relation directe à π. (voir également le dessin n°15 page 106) 1,818181 = 7 x ((π – (π/11))/11) |
| 440 / 2 = 220 220 / 11 = 20 20 / 11 = 1,818181 |
280 / 7 = 40 40 / 7 = 5,7142857 = π x 1,818181 40 / 11 = 3,636363 40 / 22 = 1,818181 |
La fraction par dix pour 440 et 280 ne permet pas de dessiner la géométrie du cercle. |
| 440 / 3 = 146,666 440 / 6 = 73,333 |
280 / 3 = 93,333 280 / 6 = 46,666 |
Ces deux fractions montrent que la division par trois et par six n’existe pas dans la proportion du nombre de coudées contenue dans chaque mesure. π n’est pas relatif à l’hexagone mais à la proportion de 7 et 11. Toutefois, il faut remarquer que la longueur de la base divisée par trois donne la mesure correspondante en mètre de la hauteur de la pyramide. |
| 484 / 2 = 242 242 / 11 = 22 22 / 11 = 2 |
308 / 2 = 154 154 / 7 = 22 22 / 7 = π |
484 et 308 sont le nombre de coudées contenues lorsque celles-ci mesurent 0,47619048 mètres. Cette coudée est contenue 3,3 fois dans la valeur π/2 , 6,6 fois dans la valeur π, et 13,20 fois dans la valeur 2π. 0,47619048 x 3 = 1,4285712 = 10 x (π/22) 1,4285712 / 11 = 0,1298701 = 3,666666 x 0,4761904 (voir dessin n°15 page 106). 0,1298701 x 14 = 1,8181815, soit la proportion de 280 / 154 et 440 / 242. 0,47619048 / 10 x 11 = 0,5238094. |
| 484 / 22 = 22 22 / 11 = 2 2 / 2 = 1 |
308 / 22 = 14 14 / 11 = 1,272727 = 4/π |
2 et 4/π sont les proportions de la pyramide qui permettent d’obtenir la fraction de la base sur la hauteur = 1,5714286. |
| 484 / 22 = 22 22 / 11 = 2 |
308 / 11 = 28 28 / 11 = 2,545454 |
2,545454 divisé par 2 = 4/π. En divisant 4 unités à la base et 2,545454 en hauteur, la fraction est 1,5714286. |
| 484 / 44 = 11 11 / 11 = 1 |
308 / 28 = 11 11 / 11 = 1 |
Le rapport de proportion est ici celui du rayon et du quart de cercle. Les deux fractions par 44 et 28 permettent d’atteindre l’unité de 0,47619048.. |
| 484 / 4 = 121 121 / 11 = 11 11 / 11 = 1 |
308 / 4 = 77 77 / 7 = 11 11 / 11 = 1 |
440 / 4 = 110; 110 / 11 = 10 280 / 4 = 70; 70 / 7 = 10 Ces deux fractions sont à comparer à la première série de calcul où la coudée royale de 0,5238095 n’est exprimée qu’à la puissance 10. |
| 484 / 28 = 17,285714 17,285714 / 11 = 1,5714286 |
308 / 22 = 14 14 / 7 = 2 |
Ce rapport de proportions est celui du dessin n°5. |
| 484 / 11 = 44 44 / 11 = 4 |
308 / 7 = 44 44 / 11 = 4 |
Ces deux fractions montrent la valeur égale de l’unité sur la hauteur et la longueur du côté de la pyramide. |
| 484 / π = 154 = 308/2 154 / 7 = 22 |
308 x (π/2) = 484 484 / π = 154 |
Dessins n°11 à 13. |
| 484 / 3 = 161,333 484 / 6 = 80,666 |
308 / 3 = 102,666 308 / 6 = 51,333 |
Ces deux fractions montrent que la division par trois et par six n’existe pas dans la proportion du nombre de coudées contenue dans chaque mesure. π n’est pas relatif à l’hexagone mais à la proportion de 7 et 11. |
1, 5, 7, 11, 14, 22, 28, 50, 70, 100, 140, 200, 220, 280, 440. A ces valeurs, viennent s’ajouter celles de 484 par 308 coudées. Leur fraction jusqu’à l’unité permet toutes les combinaisons de calculs et de dessins pour exprimer la portion de chaque mesure de la pyramide. Toutefois, si l’unité la plus petite trouve valeur dans le nombre 1, l’échelle de la coudée telle qu’établie dans la valeur de (0,523809534 x 10) est onze fois plus grande que la coudée, non plus de 0,523809534 mais 0,47619048. Le multiple par onze de 0,47619048 est 5,23809534, compté 44 par 28 fois dans une proportion à l’échelle humaine pour trianguler toutes les fondations.
Trois fois cette valeur de 10 coudées de 0,523809534 mètres donne la proportion de 10(π/2), six fois celle de 10π et douze fois celle de 20π pour un cercle de rayon 10 mètres et de diamètre 20. Le périmètre du cercle est 440/7, le demi périmètre 220/7 et le quart de cercle 110/7. Dans chacune de ces proportions de π, le nombre 11 multiplie l’unité de 10/7.
Le double de 5,23809534 est 10,47619070 (). Trois fois cette valeur est comprise 14 fois dans la longueur de la base de 440 mesurée en coudées et six fois cette valeur est contenue sept fois. Dans la longueur de 484 coudées, cette mesure est comprise 15,4 et 7,7 fois la conversion étant celle de la coudée au mètre. Le cercle dont l’unité hexagonale portée sur le cercle est de 10,47619070 mesure 10 de rayon, 20 de diamètre et son périmètre mesure 440/7. Le nombre 11 est contenu dans la proportion unitaire de 10/7, la valeur de 10 étant π/3 fois plus petite que celle de 10,47619070.

Lorsque l’on considère toute la proportion de la pyramide, la valeur de “π” est exprimée par l’unité de 69,14285714 coudées, contenue 7 fois dans la longueur de la base de 484 et 14 fois dans le demi-périmètre du cercle de rayon la hauteur.
(308 x π)/14 = 69,14285714 = 22π
Dans la longueur de 440, le nombre “π” est exprimé dans la valeur 62,8571428 contenue 7 fois dans la base et 14 fois dans le demi-périmètre.
(280 x π)/14 = 62,8571428 = 20π
Les nombres se multiplient, se divisent, s’additionnent et se soustraient dans ce pur équilibre de la valeur de l’unité dont la constante π est invariable dans le dessin d’une fraction d’un cercle par l’unité qu’il contient. 7, 14, 28 et 11, 22, 44 sont les mesures célestes qui arrondissent les angles, par 360 comptés, et en 7 divisés. 51°42’85”71”’ devrait être la véritable inclinaison de quatre arêtes qui font apothèmes correspondant à chaque points cardinaux.

C’est en dessinant le plan de la pyramide, que l’on peut mieux apprécier l’utilité d’une mesure qu’il est possible de reproduire suivant le ratio constant de 11 pour passer successivement de 0,4761904 à 5,2380952 puis 57,619048 contenu 4 fois dans la largeur de la base. Ces valeurs exprimées en mètres font 1 x 11 x 11 x 4 pour la largeur de la base et 1 x 7 x 2 x 11 x 2 pour la hauteur. Lorsque la base mesure 484, sa racine est de 22, contenue 14 fois dans la hauteur. Lorsque la hauteur mesure 308, la fraction par 2π donne le carré de 7 dont la racine est contenue 22π fois dans la largeur de la base.
Les valeurs irrationnelles des mesures ainsi exprimées par les nombres de coudées trouvent similairement à l’écriture de π une simplification décimale dans les nombres fractionnaires dont l’unité entière est inscrite par la main. Le pouce, la paume et la coudée, sont des proportions à l’échelle humaine qui toutes signifient 1. Lorsque la coudée mesure 0,4761904 mètres, l’écriture fractionnaire de 10/21 donne 2,267573 centimètres pour le pouce, 22,67573 centimètres pour la paume, et 11/21 pour le dixième de 11 coudées de 0,4761904 , soit la coudée royale de 0,5238095 mètres. Cette fraction de 11/21 multipliée par 11 donne 121/21 pour le dixième d’une longueur du quart la largeur de la base, soit 10 fois 484/21. Lorsque l’on convertie 484 coudées par le nombre de mètres correspondant, les premières décimales de 230,47619 sont celles de la coudée de 0,4761904 mètres, celle-ci étant multiple de 10 par 21.
Ces nombres fractionnaires exprimés en mètres facilitent les convertions dans les proportions de Khéops, pour en traduire chaque unité, chaque multiple, et chaque proportion entière relative aux dimensions connues dans un rapport de mesures qui confondent les décimales. Evincées, elles n’expriment plus que l’invisible quantité de nombres contenus dans la limite du métre, entier divisé et multiplié par 10/21.
21 est le produit de trois mesures de 7, et 1 l’unité par laquelle arriver à π pour inscrire en mémoire toute l’ampleur de nombres qui pierre par pierre s’ajoutent un à un. De 10/21 à 11 fois cette fraction il suffit d’ajouter 1 pour en trouver le dixième qui de 11/21 se transforme par 2 pour faire le carré de 11 qui s’inscrit deux à deux.
| 1 | 0 | |
| 1 | 1 | |
| 1 | 2 | 1 |
| 4 | 8 | 4 |
Ces nombres, sur trois unités de 7 construisent tout le plan de la pyramide métrée par une seule valeur de logique fondée sur le dessin d’une ligne tracée au compas. De la courbe à la ligne droite, la multiplication est celle de 11 qui fait le carré de son double depuis la base jusqu’au sommet.
Les conversions deviennent plus simples lorsqu’il suffit de multiplier 484 par 10 puis diviser par 21. Les décimales de 230,476190476, sont les mêmes que celles de la coudée de 0,476190476 que l’on retrouve dans la fraction de π/3 = 1,0476190476. Cette valeur de π/3 est de 22 fois le 1/10ème de la coudée de 0,476190476 et 230,476190476 est 22² fois la valeur unitaire de cette coudée. Dans la hauteur de la pyramide le produit de 308 par 10 donne 3080 pour résultat, que l’on divise par 7 pour arriver à 440 puis par 3 jusqu’à 146,66666 mètres.
Toutes ces propriétés de la valeur de la coudée de 0,4761904 mètres obéissent également à une géométrie du cercle comparable à celle de la coudée royale de 0,5238095 mètre. Mais au lieu d’être inscriptible dans le dessin d’un cercle de rayon 1, le dodécagone dont l’arc mesure 0,4761904 est inscriptible dans un cercle de rayon 0,909090 mètres. L’hexagone est inscrit dans un cercle de rayon 0,454545 mètres dont chaque segment est π/3 fois plus petit que 0,4761904.

= 0,636363 x (π/22)
= (7/11) x (π/22)
9,090909 x 2 = 18,181818
= 10 x 1,818181
= 127,272727 x (π/22)
= 100 x (4/π) x (π/22)
Fig.16 – La valeur de 0,909090 est celle de 10 mètres divisés par 11, celle de 0,454545 est de 10/22.
Le quart de périmètre du cercle de rayon 0,909090 mesure 10 (π/22), celui de rayon 0,454545 mesure 5 (π/22). Ces deux valeurs du périmètre sont proches de 7 et 14 aux décimales de (π/22) près. Si le quart de périmètre de longueur 5 (π/22) avait mesuré 7, chaque unité portée sur le rayon aurait mesuré 0,636363, valeur dix fois inférieure à celle de (0,909090 / (π/22)).
Si l’on divise le rayon du cercle de diamètre 9,09090 en 20 unités plus petites, chaque unité mesure 0,454545 centimètres. Si l’on ajoute 4 à l’unité de 0,454545, on obtient la valeur du rayon du cercle dont le quart de périmètre mesure 7. Chaque unité de 1/7ème 4,454545 mesure 0,636363 et 11 unités font 7. De même, lorsque l’on divise le diamètre du cercle de rayon 9,09090 en 5 unités, celles-ci mesurent 1,818181, soit 10((4/) x (π/22)).
Lorsque l’on divise 4 par 0,909090, on obtient un résultat de 4,4. Lorsque l’on divise 44 par 0,909090, on obtient 48,4. Cela revient à dire que le résultat de 11 pour 484/44 implique que la fraction de 10/11 correspondant au rayon du cercle par lequel déterminer la valeur de la coudée de 0,4761904 est le produit de la division.
44 / (1/11) = 484
484 / 44 = 11/1 = 11
La valeur de 0,4761904 est celle de 10(π/22) divisée par 3, soit 10/21. L’arc de cercle de longueur 0,4761904 est π/3 fois plus grand que le rayon du cercle de 0,454545.
Il est ici intéressant de comparer chaque unité à celles qui définissent la valeur universelle du mètre. Dix millionnième partie du méridien boréal, le mètre est synonyme de la division du quart de périmètre du cercle terrestre par une mesure décimale. Lorsque l’on divise le rayon du cercle de 0,909090 en 7 unités, celle-ci mesure 0,12987013. Cette valeur exprimée en mètres est 100 000 000 fois plus petite que 12 987,013 kilomètres, longueur que les égyptiens auraient pu évaluer comme Delambre et Méchain en mesurant une partie seulement du globe terrestre pour déterminer la longueur de son diamètre. Lorsque l’on soustrait le diamètre équatorial de la Terre de 12 756,280 au diamètre hypothétique qui aurait pu en être évalué, la différence de 12 987,013 – 12 756,280 est de 230,73299 kilomètres, valeur proche de celle exprimée en mètres dans la largeur de la base de Khéops.
Si le diamètre équatorial avait pu être évalué à cette époque au nombre de 12 987,013 kilomètres, le périmètre terrestre aurait dû être celui de 40 816,3266 kilomètres, pour un quart de périmètre long de 10 204,0816 kilomètres. Si l’on applique le mode de division effectué pour la largeur de la base de la pyramide à celui du périmètre terrestre,
10 204,0816 divisé par 4 mesure 2551,0241 kilomètres, divisé par 11, cela fait 231,910946 kilomètres, puis par 4, on arrive à 57,9777366 kilomètres, puis 11, cela fait 5,27070333 kilomètres, puis 11 pour arriver à 0,479154848 kilomètres. Cette valeur est 21296 fois plus petite que le quart de périmètre équatorial. La racine de 21296 est 145,93149 kilomètres, valeur proche de l’expression en mètres de la hauteur de Khéops.
Inversement, si l’on exprime la valeur de la coudée de 0,4761904 en kilomètres, le produit par 21296 donne un quart de périmètre terrestre de 10 140,9524 kilomètres pour un diamètre équatorial de 12 906,6667. La différence avec la vraie longueur du périmètre terrestre est de 150,38667 kilomètres. De même, lorsque l’on divise le quart de périmètre théorique de 10 204,0816 kilomètres par π, la valeur est de 3246,7532 kilomètres, à 36,948833 kilomètres près la position de Khéops sur la surface du globe, correspondant à une latitude de 28°63’63”63”’ degrés. Avec un quart de périmètre terrestre de 10 140,9524 kilomètres, la division par π fait 3226,66667 kilomètres à 57,03533 kilomètres près la position réelle de Khéops. La distance de 3246,7532 kilomètres correspond au produit de 75000/11 coudées de 0,4761904, soit 6818,181818 fois la fraction de 10/21, ce qui représente une distance de Khéops à l’équateur de 750 000 /231 coudées. La fraction étant celle par 11, 3226,6666 kilomètres correspondent au quart de périmètre d’un cercle dont le périmètre complet est de
12 987,013 kilomètres, soit 100 000 fois le diamètre de 0,909090 / 7.

Le rayon équatorial mesure 6 493,5065 kilomètres = ((0,909090 / 7) / 2) x 100 000.
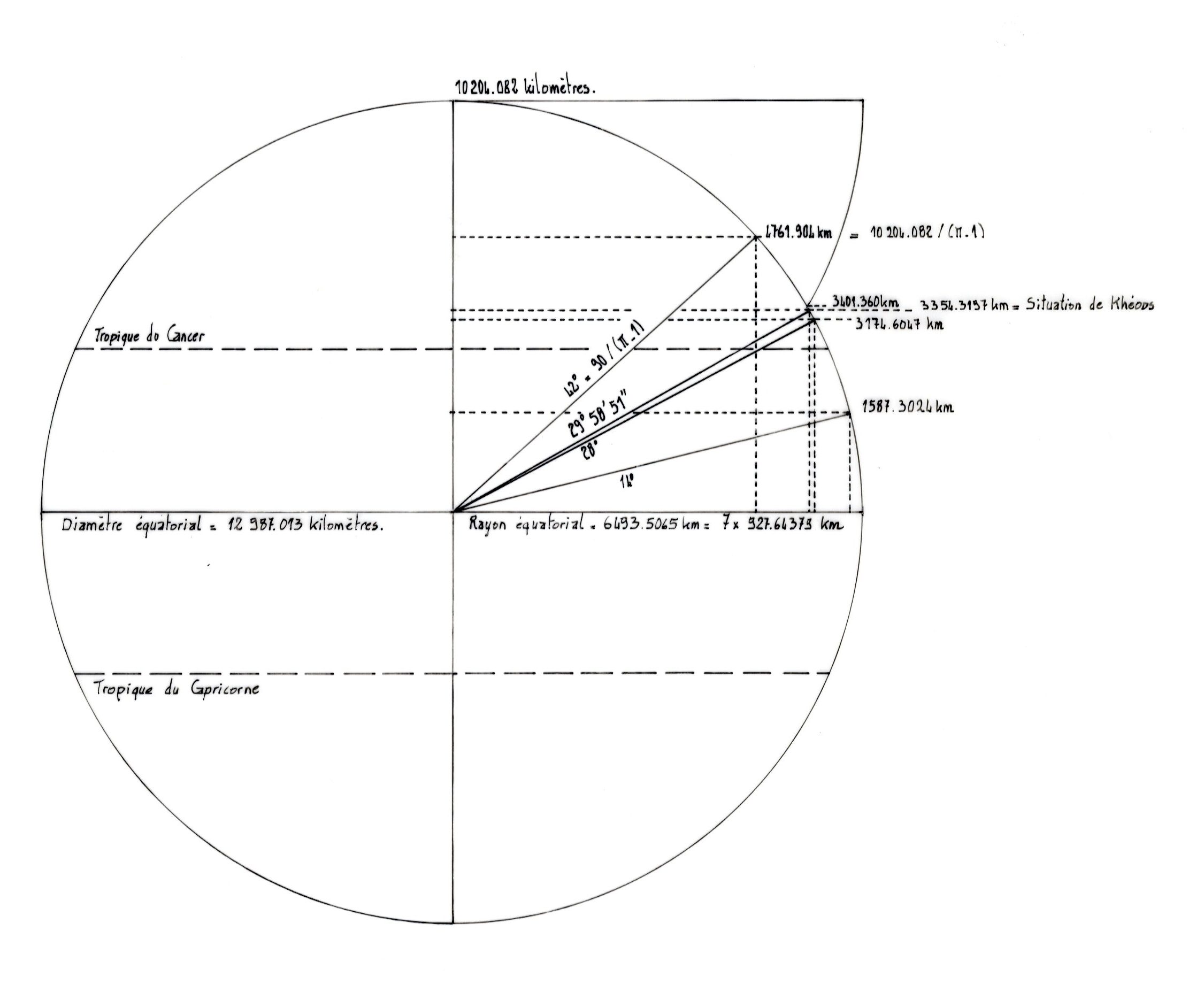
La position de Khéops est de 29°58’51” degrés Nord, soit 3354,3197 kilomètres jusqu’à l’équateur. La différence avec la situation réelle de Khéops est de 71,617689 kilomètres.
Le quart de périmètre de la Terre mesure 10 204,082 kilomètres.
Le tiers de 10 204,082 est de 3 401,3605 kilomètres, soit une différence de 47,040806 kilomètres avec la situation de Khéops.
Le tiers du quart de périmètre terrestre divisé par 10 puis multiplié par 14 mesure 4 761,904 kilomètres, soit 10 000 fois la valeur de 0,4761904. L’angle d’inclinaison de 4 761,904 est de 42 degrés soit 90/(π – 1). Chaque degré terrestre mesure 113,37874 kilomètres.
Lorsque l’on divise 42 degrés par 2 puis par 3 on obtient la valeur de 7 degrés contenue 6 fois dans l’arc de longueur 4 761,904 kilomètres. Lorsque l’on divise
4 761,904 par 6 puis 7 le résultat est donc la valeur du degré.
42 /2 = 21
21 / 3 = 7
4 761,904 / 6 = 793,65117 km
793,65117 / 7 = 113,37874 km
113,3787 x 90 = 10 204,082 km
La valeur de 42 degrés multipliée par (π/22) est de 6 soit le nombre de côtés du polygone dont le périmètre mesure 42 pour un cercle de rayon 7. Lorsque l’on divise 42° par 3, la valeur de 14° mesure 1 570,9214 km de latitude soit une longueur sur le périmètre terrestre de 1 587,3024 km. La latitude de 28° est de 3 048,5166 km, soit 3174,6047 km porté sur le périmètre. La différence avec la position de Khéops est de 179,715 kilomètres.
Toutes ces valeurs hypothétiques d’une géodésie terrestre montrent l’extrême sensibilité des mesures du globe faisant seulement varier de quelques kilomètres une géométrie qui aurait pu être dessinée sans volonté nécessairement immédiate. Les pyramides de Saqqara, puis Meïdoun et Dahchour se trouvent au Sud du complexe de Guizeh. Guizeh n’est pas situé à l’embranchement du delta du Nil, mais sur la rive Ouest du Bahr Youssouf qui alimente le Lac Karoûn et conduit jusqu’à l’estuaire d’Alexandrie. La position de Khéops à 29°58’51” degrés ne signifie rien d’une géométrie conçue qui puisse s’insérer au dessin du cercle par quelques rapports de fraction. Comparativement 90/π mesure 28°63’63”63”’, et 90/3 mesure 30°. Khéops se situe à l’intermédiaire de deux fractions qui ont une géographie essentiellement terrestre, par le dessin morphologique de la Terre à cet endroit des rives du désert.
Peut-être faut-il voir la nécessité moins abstraite de la situation de Guizeh imposée par l’ensemble des procédés d’inhumation de l’époque. Le corps lavé dans l’eau du Nil ne pouvait exposer aux risques microbiens, ce qui implique que la momification ait dû être effectuée en aval des villes, sur le cours mineur du Bahr Youssouf où l’eau risquait moins d’être consommée.
Seul le doute fait ici certitudes, sans volonté de convaincre par quelques valeurs la vraie nature des connaissances que pouvaient avoir les égyptiens. Les démonstrations précédantes parlent par elles-mêmes, et nul besoin n’impose de justifier ici les résultats obtenus par une géographie qu’il reste improbable de pouvoir vérifier. Mais la synthèse des nombres impose d’elle même tout le superflux de la découverte, seulement pour rappeler que pour être conçue, l’architecture est une géographie.
Le choix de l’orientation de Khéops atteste la valeur des connaissances de l’époque pour déterminer à la minute près, la position du Nord vrai, et il se pourrait, qu’effectivement, les égyptiens aient su mesurer la Terre suivant des principes ampiriques qui restent à devoir être démontrés. Savoir si en concéquence ces théories auraient pu affirmer une volonté de construire Khéops dans les proportions d’une unité terrestre demeure en contradiction avec l’objet de cette étude. L’unité déterminée dans les cinq séries de calculs affirme une objectivité qui se peut être démontrée par la pratique de dessins en cohésion à la logique d’une valeur mathématique qui admet une géométrie. Le nombre π est un rationnel qui permet le développement d’une analyse géométrique essentiellement évolutive, pour comprendre d’une part, quelle pouvaient être les connaissances de l’Egypte, et tenter d’autre part de mettre en valeur une géométrie. Le dessin permet de déployer en conséquence le développement d’une hypothèse qui se veut être démontrée pour dépasser le préjugé de valeur couramment admises et tenter de développer une étude plus aboutie. Cela implique nécessairement de dépasser le stade graphique de l’observation pour tenter au cours des pages de construire une objectivité qui par séries de démonstrations puisse permettre d’évoluer vers le fondement de théorèmes qui fassent preuves de solidité.