L’ensemble des proportions énoncées, nous avons vu que les mesures de la coudée royale correspondaient au dessin d’un cercle dont le rayon de longueur 1 permettait de définir une valeur de π = 3,14285714. Les proportions du cercle dont le rayon mesure 1 sont divisibles dans les proportions de la pyramide dont la moitié de la hauteur définit le quart de périmètre de longueur 11. Similairement, la hauteur de la pyramide définit la longueur du diamètre dont le demi-cercle est la base de Khéops. Toutes ces valeurs, converties suivant les proportions de Khéops, permettent de définir le dessin d’une règle dont la base mesure 1,57142857, la hauteur 2, ces deux valeurs étant divisibles en nombre d’unités convertibles par les entiers 11 et 14.
L’expression de π, telle que nous la connaissons, transparaît différemment à l’énoncé des premiers dessins. N’exprimant aucun rapport entre le périmètre du cercle et la longueur de son diamètre, la valeur de π est ici un rapport unitaire du rayon permettant de définir par le dessin d’une droite la longueur approchée de son périmètre. Le rayon d’un cercle étant divisible en nombre entier d’unités plus petites, la proportion de π pour chaque unité est celle qui permet de définir le nombre entier de ces unités contenues sur la longueur du périmètre. Lorsque le rayon mesure 7, le quart de périmètre mesure 11 unités de longueur égale à celles du rayon.
Sachant que la coudée royale est inscriptible dans le dessin d’un cercle dont le rayon mesure 1, il en va implicitement de même dans le dessin de la règle dont la base mesure 1,57142857. Les régulations doivent cependant être trouvées pour tenter de comprendre quelles lignes directrices permettent d’établir une géométrie dans laquelle toutes les valeurs mathématiques puissent être vérifiées.

Toutes ces régulations impliquent qu’une corrélation existe entre la hauteur de 2 et la valeur de la coudée différemment de celle préalablement définie dans le dessin du cercle. Partant de ce dessin, on peut émettre l’hypothèse qu’il existe un tracé pour définir la coudée sur la hauteur de 2 afin que le dessin puisse mettre en relation toutes les régulations proportionnelles à π.
Reprenant le dessin précédent, la demi-section méridienne de Khéops est dessinée dans les proportions des deux règles de 1,57142857 et 2 suivant un rapport exprimé en coudées de 220 par 280. Le triangle rectangle obtenu est divisé en deux sur sa hauteur, permettant ainsi de tracer deux carrés de hauteur 1 et par conversions 140, 70 ou 7. La diagonale du carré dont le côté mesure 140 est coupée par l’arc de cercle de rayon 140, ce qui permet d’obtenir le point d’intersection correspondant à chacune des valeurs de
140/√2 = 98,994949, 1/√2 = 0,7071067, 70/√2 = 49,497475 et 7/√2 = 4,9497475.

En divisant la hauteur du carré de longueur 140 en sept unités égales, on peut tracer la droite passant par la sixième unité verticale et le point d’intersection obtenu entre la diagonale et l’arc de cercle de rayon 140. La hauteur de cette droite à la verticale de l’extrémité du triangle est égale au tiers de la longueur de la base, ce qui permet de dessiner trois carrés dont la hauteur est proportionnelle à la coudée royale. Cette hauteur est 1/2 de 140 auquel on ajoute (πr – 3r)/6 = 73,33333. Avec un rayon de longueur 1, le demi-rayon mesure 0,50 auquel on ajoute (π – 3)/6. Le résultat est celui de la coudée royale dont la longueur mesure 0,5238095.
Si l’on convertit les proportions de ce dessin suivant celles de la règle de 1,57142857, chaque unité de onzième la longueur de la base du triangle mesure 0,14285714, soit la valeur approchée de π/22. Cette valeur équivaut également à 1 divisé par 7, le nombre d’unités qu’il faut dans un rayon de 1 pour obtenir la longueur exacte de son quart de périmètre lorsque cette valeur est reportée 11 fois, la longueur du demi-périmètre lorsque cette valeur est reportée 22 fois, et la longueur du périmètre complet lorsque cette valeur est reportée 44 fois. Il est donc possible d’exprimer les valeurs de π suivant un rapport fractionnaire du rayon.
2π = 44/7
π = 22/7
π/2 = 11/7
Il en résulte que quelle que soit la longueur du rayon, le septième de sa mesure vaut πr/22. Inversement, quelle que soit la longueur du rayon, 44 fois le septième de sa mesure donne la longueur du périmètre du cercle. Donc π = (44r/7)/2r= 44/14 pour le rapport au diamètre ou 22/7 dans la proportion du rayon. Similairement, π/2= 44r/28r = 11/7 et 2π= 44r/7r = 44/7. Il est donc possible d’exprimer les valeurs décimales en fractions de nombres entiers, lorsque les nombres décimaux sont des rationnels périodiques.
En comparaison au dessin n°2, si l’on considère que la longueur de la base est le périmètre d’un cercle de 440 coudées, chaque unité portée sur le périmètre mesure 10 coudées de 440/44 soit 5,2380953 mètres. Le rayon du cercle de périmètre 440 mesure 70 coudées dont la mesure convertie en mètres est de 36,66666. Cette valeur est égale au tiers de 110, non plus compté en coudées mais en mètres. Cette valeur exprimée en mètres équivaut à 210 coudées, soit la somme des trois côtés d’un hexagone lorsque
π = 3.
Si l’on considère que 1,57142857 est la valeur de π/2 pour un cercle de rayon 1, cela revient à dire que 1,57142857 est la valeur de π pour un cercle de rayon 0,5. Cette valeur du rayon est égale à la longueur de la coudée royale divisée par π/3. Lorsque l’on divise 110 mètres par le nombre d’unités de 0,5, on obtient un résultat de 220, soit la moitié de 440. De même, 220 x (π/3) = 230,47619, soit la longueur de la base de Khéops.
Il faut remarquer ici les relations entre les nombres lorsqu’ils sont exprimés en mètres ou en coudées. Le rayon du cercle de périmètre 440 mesure 70 coudées. Cette valeur multipliée par π/2 est égale à 110 coudées. La valeur de 110 est également le nombre de mètres correspondant à trois longueurs de rayon du cercle lorsque l’on convertit 70 en 36,66.
36,66 x 3 = 110
70 x 3 = 210
La différence de 210 coudées à 110 mètres est de 6/π, soit la proportion du mètre par rapport à la longueur de la coudée royale et celle de 440 comparée au nombre de mètres correspondants.
210/110 = 1,909090 = 6/π = 21/11
0,52380952 x (6/π) = 1 mètre.
440 / (6/π) = 230,476190 mètres
Si l’on multiplie 36,66 par π/2, on obtient une mesure égale à 110 coudées royales soit 57,6190476 mètres. Cette valeur multipliée par 4 puis par 6/π est égale à 440. Cela revient à dire que multiplié par 12, le rayon du cercle exprimé en mètres permet d’obtenir la longueur du périmètre exprimé en coudées.
36,66 x 12 = 440
Inversement, chaque longueur de périmètre exprimée en coudées donne la valeur correspondante du rayon exprimée en mètres.
440 / 12 = 36,66
6/π = 21/11
π/3 = 22/21
2π/3 = 44/21
L’ensemble de ces calculs permet de définir une valeur fractionnaire de la coudée royale dont l’expression π/6 = 0,5238095 est réduite à plus simple écriture due aux propriétés unitaires de la valeur de π. Avec π = 22/7 l’expression de la longueur du périmètre sur celle du rayon permet de retraduire le contexte du dessin suivant la division du demi-périmètre en six segments égaux.
π/6 = 11/21 = 0,5238095
La valeur de la coudée royale écrite par la fraction de 11/21 correspond à la longueur du périmètre d’un cercle de rayon 7 divisée par la somme de trois longueurs de rayon. Le dessin est celui de la page 68 (fig.3) où la division du quart de périmètre en trois segments égaux permet de définir le dessin du dodécagone dont chaque arc mesure une coudée.

Reprenant le dessin n°5, il faut également remarquer l’ensemble des proportions qui définissent cette géométrie. La base du triangle de longueur 1,57142857 divisée en 11 unités mesure en hauteur 14 unités dont la somme des unités fait deux. La hauteur du triangle divisée par 4 mesure le tiers de la base lorsque chaque carré défini sur la base est multiplié par π/3. La hauteur de 2 divisée par un tiers de la base établit la proportion de 12/π.
Lorsqu’on ajoute un quatrième carré aux trois carrés de base, les diagonales de ce carré définissent avec le point d’intersection de la diagonale et l’arc de cercle de rayon 140 un point sur l’axe vertical de hauteur le centre du cercle exinscrit au triangle. Les sommets de hauteur 2 et de longueur 1,57142857 sont situés sur le cercle de rayon 1,617347 dont la hauteur du centre est de 0,382653. Ces valeurs algébriques voisinent celles obtenues par le dessin à 0,000419038 près, l’imprécision étant due au principe du dessin dont les régulations ne peuvent permettre aucune démonstration géométrique. Le centre du cercle défini par le dessin est de 0,382234, le rayon mesure 1,618866 qui à l’échelle de la pyramide présente une erreur de 3,07308 centimètres. Dans le dessin de la pyramide, le centre du cercle est situé à une hauteur de 53,571428 coudées et le rayon mesure 226,42857 coudées, valeurs proportionnelles aux décimales de π. Ces valeurs exprimées en mètres sont de 28,061223 et 118,60544 mètres.
Bien que le dessin ait une approximation relative pour définir la valeur exacte du centre du cercle, les comparaisons avec la coupe de Khéops laissent à penser que le centre du cercle ait pu servir à définir toutes les régulations intérieures. Les couloirs, la Grande Galerie et la disposition des chambres sépulcrales correspondent à un dessin dont le tracé est orienté sur le centre. Les démonstrations sont illustrées par les dessins n°17 et 18.
De l’ensemble des valeurs préalablement établies, il faut également remarquer le rapport défini entre le ratio de π et l’expression de ses décimales. La différence de longueur entre le quart de périmètre et le nombre de fois que le rayon est reporté est d’une demi-unité de 1/7 soit 0,0714286 = (0,1428572 / 2). Lorsque l’on ajoute à chacune de ces valeurs le nombre de fois que le rayon est reporté, on obtient respectivement 1,57142857 et 3,14285714 soit π/2 et π pour un quart et un demi cercle de rayon 1. Il en résulte que le septième d’unité du rayon est égal à la valeur (π-3) de ce rayon.
Lorsque l’on compare la hauteur de la pyramide à la longueur de la base, le rapport de 14/11 est de 11 unités de longueur 1,272727 dans la hauteur de 14. Cette mesure quantifiable par la valeur unitaire de 14/11 trouve écriture également inscriptible dans la proportion de π. Cette valeur de 1,272727 correspond à 4 longueurs de rayon divisées par la longueur du demi-périmètre du cercle de rayon 7. La fraction est de 4/π, valeur soulignée par l’importance avec laquelle elle permet d’écrire la plupart des résultats qui suivent en rapports simples d’entiers dont la rationalité facilite l’essentiel des calculs par le dessin.
(π/2) x (4/π) = 2
Cette équation sans inconnu permet de définir la valeur du diamètre dessiné sur le demi-périmètre du cercle. Onze unités d’un diamètre de 14 multipliées à 4/π mesurent la longueur du diamètre. Le quart de périmètre du cercle est donc 4/π fois plus petit que son diamètre, de même que le quart de périmètre est π/2 fois plus grand que le rayon. L’ensemble de ces fractions déterminent l’expression unitaire du rayon par 7, 11, 14, 22 et 44.
Propriété élémentaire de cette géométrie, la fonction mathématique en définit malgré tout l’importance primordiale de pouvoir mesurer chaque valeur dessinée en rapports unitaires qui puissent être démontrés. L’objet de π est la manifestation évidente de pouvoir déterminer le moyen de mesurer ce qu’aucune mathématique ne rend visible à l’oeil. Le cercle est dessiné autour de son centre pour tracer une ligne qui en détermine le rayon. Le rayon est divisé en 7 unités constantes qu’une ligne multiplie 44 fois sur le périmètre. Cette ligne tracée, il suffit de la dérouler pour que quarante unités circulaires deviennent des segments de droite. De là un dessin, celui pyramidal de la valeur du cercle quadrangulé par π.
S’il semble évident que l’écriture fractionnaire de 22/7 efface toutes les décimales infinies de π, la phonétique n’admet cependant qu’un langage usuel pour exprimer concrètement la géométrie du cercle qu’il convient d’arrêter au dessin d’une seule mesure, celle du rayon de 7. De là, toutes les lignes mémorisables dans le trait d’un seul nombre trouvent leur développement remarquable dans la courbe du cercle qu’une simple expression de 4 et 3 permet de retrouver facilement. Jeu enfantin du rythme des mots , tous les calculs s’en suivent de logique par la pratique du dessin afin que connaître soit une manière de comprendre tous les mystères cachés de la géométrie. La féerie de Khéops embaume la pensée par tout le temps qu’il fallut de découvertes, prétexte fabuleux pour parvenir en ce siècle à mettre la géométrie sur le tableau d’honneur, celui oublié des Sciences que la géométrie a précédées.

S’il est aisé de faire le tracé d’une géométrie de la coudée royale, l’opportunité de pouvoir en déterminer le nombre implique cependant que le cercle ait pu être mesuré suivant une seule valeur définie par le mètre. Adopté par la Convention Nationale de 1795, le mètre définit théoriquement la dix millionnième partie du méridien allant de l’équateur au pôle boréal , suivant un système décimal qui le divise par le décimètre et le centimètre. Aucune de ces valeurs ne pouvait être connue des égyptiens, ce qui implique une redéfinition de la valeur de la coudée.
Pour comprendre l’importance du dessin géométrique de la coudée, il faut parvenir à ressituer l’ensemble des mesures dans le contexte de leur époque en développant la logique qui aurait pu prévaloir à la définition d’un système métrique élaboré. Les valeurs jusqu’alors admises pour la coudée royale aident en ce sens à déterminer le dessin qui permet d’inscrire une valeur théorique dans le tracé d’une géométrie de π. Mais si juste en soit l’hypothétique dessin, sans doute faut-il préalablement réviser l’échelle définie dans l’étude qui suit par nécessité d’en trouver l’ultime valeur.
Implicitement régulée par une conception de l’espace qui devait tenir compte de l’échelle humaine, la coudée royale est un concept naturel de l’unité souveraine dans un monde construit. Géométriquement défini par la courbe du cercle, les égyptiens ont inventé un système linéaire permettant de réguler par mesures entières toutes les géographies de l’Egypte unifiée. De la mesure la plus petite à celle définie la plus grande, il semble évident qu’il y ait eu un principe pour réguler chaque changement d’échelle, suivant un mode de conversion conçu pour être dessiné dans le cercle entier. En comprendre l’éventuelle géométrie nécessite de parfaire le dessin de la coudée telle qu’admise jusqu’alors comme mesure métrique pour effectuer tous les calculs de conversions. Proche de la demi-mesure d’un mètre, l’expression de la coudée royale permet facilement de traduire une idée des mesures accordées au dessin, mais si simple en soit le procédé linguistique , l’étude historique implique réfléxions qui puissent parfaire l’harmonie de l’oeuvre par celle harmonieuse d’un système de mesures.
Intimement impliqué dans le développement historique d’une Egypte savante et novatrice à la fois, le système de mesures contribua essentiellement à définir le concept d’une géométrie. L’évidente manifestation en fut transmise par Khéops, que l’étude permet d’inscrire dans le dessin dépouillé de toutes les connaissances culturelles pour en rechercher l’authentique volonté. Le tracé du cercle fut sans doute l’objet de toutes les mesures qui lui furent attribuées, et l’étude des mesures telles relevées sur le site permet d’en créer de plus amples desseins.
Le but essentiel de comprendre la géométrie de Khéops implique que toutes éventualités puissent faire suggestions d’une étude historique qui ne peut s’affirmer que par fouilles comparées dans l’esprit des formes. La pyramide signifie la volonté affirmée de mettre en oeuvre les pratiques d’un savoir, conçu dans la géométrie matricielle des formes que l’architecture conceptuelle permet de construire. L’objet du dessin est de parcourir les concepts qui pouvaient prévaloir à cette époque pour définir quelle géométrie fut épurée à la construction de Khéops.
Il est évident que le développement de l’analyse impose d’oublier la forme du dessin, l’élaboration d’une géométrie étant seul moyen d’affiner la recherche. Mais il ne faut pas pour autant omettre le fait que les égyptiens aient pu surpasser tout ce que la Grèce pu transmettre plus tard dans son enseignement. L’Egypte des Pharaons, su développer un concept unique de conservation de tous les savoirs par la vue qui en était donnée. La forme mystique de l’architecture à cette époque traduit une volonté de montrer ce que les textes ne peuvent écrire. Le secret pu être formulé dans la forme figée des pyramides qu’aucun pillage ne pouvait dérober à la connaissance de ses constructeurs. La transmission orale des savoirs de cette géométrie impliquait d’en connaître l’ensemble des préceptes fondateurs, sans quoi il ne pouvait transparaître aucune réalité de l’oeuvre qui fut accomplie dans le dessin de la pyramide.
En dérouler l’hypothétique savoir sur le fondement des connaissances acquises impose une profusion de concepts anachroniques que seule une analyse comparative raisonnée peut épurer pour en traduire l’objectivité éventuelle. Loin d’en avoir atteind les objectifs, cette étude fait l’apologie de tous les savoirs de la géométrie en l’espoir qu’une conclusion puisse permettre d’affirmer la synthèse d’une histoire de la géométrie antique.
Le tracé des dessins précédents permettant d’obtenir la mesure de la coudée royale reportée trois fois dans la longueur de la base d’un triangle rectangle régulé sur π, fut trouvé à force d’essais permettant de comprendre les régulations de Khéops dans les proportions de sa base et de sa hauteur. Si juste en soit le dessin, il faut toutefois en démontrer le fonctionnement par les résultats obtenus dans la valeur des nombres.
La coudée royale mesure 1/2 de la hauteur du rayon d’un cercle de longueur 1, ajouté de la valeur de π dans la proportion du segment égal au tiers de la longueur d’un quart d’arc de cercle. Cette proportion de π égale à (π – 3)/6 énumère la progression d’un dessin permettant de diviser la longueur d’une droite dans sa valeur établie par le cercle. Si l’on dessine cette progression dans l’espace plan d’un repère d’origine, l’axe des abscisses est divisé en 22 unités et celui des ordonnées en 14. La hauteur de la règle détermine la longueur du rayon d’un cercle dont le quart de périmètre mesure 22.

L’axe de 14 est divisé en 7 unités de 2. La droite passant par la 6/7ème unité et l’intersection de l’arc de rayon 14 avec la diagonale du repère coupe la verticale d’abscisse 22 en la hauteur de la coudée. Sachant que la coudée est proportionnelle à la moitié de la longueur du rayon, la droite horizontale d’ordonnée 7 est tracée. L’intersection de cette droite avec l’arc de cercle de rayon 14 détermine la position d’un sommet de l’hexagone inscrit dans le cercle. La longueur de l’arc en cet endroit est de 7+((14π – (3×14))/6).
Si l’on imagine que l’arc est une droite et la verticale d’abscisse 14 sa perpendiculaire, la progression du dessin permet de reporter la longueur de l’arc sur cette droite afin de déterminer la vraie grandeur de ((14π – (3×14))/6). Cette mesure, considérée comme une unité, est multipliée 6 fois, pour déterminer la longueur du rayon d’un cercle. Ce rayon est divisé en 7 unités que l’on multiplie par 11 afin d’obtenir la vraie grandeur d’un quart d’arc de cercle. Cette longueur de l’arc moins trois fois la longueur du rayon détermine une valeur qui est reportée 14 fois dans la longueur du rayon et 22 fois dans la longueur de l’arc d’un quart le périmètre du cercle.
Cette progression du dessin faisant le chemin inverse de la transcendance ((14π – (3×14))/6) permet de montrer la relation de la hauteur 6/7ème à celle de la coudée royale égale au tiers de l’arc de longueur πr / 2. Le rayon du grand cercle mesurant 14, ses 6/7ème mesurent 12 et 1/7ème est égal à 2. Six est le nombre d’unités qu’il faut pour diviser la longueur de l’arc d’un demi-cercle en valeurs égales à la coudée royale soit
44/6 = 7,33. Six est également la fraction de l’unité permettant de trouver les décimales de la coudée, ajoutées à la valeur d’un demi-rayon, soit 2/6 = 0,33.
Lorsque le cercle mesure 7 de rayon, le périmètre est de 44. La longueur du rayon se reporte 2π fois sur tout le périmètre du cercle. Lorsque le périmètre mesure 44, le segment de 6 unités se reporte 7,33 fois sur tout le pourtour du cercle. Ce nombre, qui n’est pas une mesure mais une quantité de segments comptés, nécessite pour être mesuré qu’une inversion des proportions permette de passer de la quantité à la mesure. Il s’agit de définir la vraie longueur d’un arc coupé en chaque sommet d’un hexagone. Lorsque l’on reprend le calcul inverse, 7,33 multiplié par six donne la vraie longueur du périmètre du cercle de rayon 7.
Outre le moyen de trouver la vraie longueur de la coudée royale dans la proportion de π/2, ce dessin permet de déterminer par la géométrie la longueur du rayon d’un cercle lorsque l’on connaît la mesure d’un sixième de son périmètre. Cette mesure, portée sur une ligne droite verticale, divisée par 11, puis multipliée par 7 et 3 donne la vraie longueur du rayon d’un cercle sur lequel la mesure connue est portée 6 fois sur le demi-périmètre et douze fois sur le périmètre complet. Pour que cette mesure soit multipliée six fois, il suffit de faire passer l’axe du cercle par le milieu du segment donné.

De même, si l’on considère une longueur x1 quelconque, cette valeur divisée par 3, puis par 7, que l’on multiplie par 11 donne la valeur x-2 inférieure dans la proportion de (14 / la coudée royale) soit 1,909090 = 6/π. A l’inverse, si l’on considère la longueur x1 quelconque, cette valeur divisée par 11, multipliée par 7 puis 3 donne la valeur x2 plus grande que x1 dans la proportion de 6/π. Si l’on écrit cette suite, on obtient:
x1 /11 x 7 x 3 = x2 / 11 x 7 x 3 = x3
x1 / 3 / 7 x 11 = x-2 /3 / 7 x 11 = x-3
Avec x1 = la coudée royale, (x1 = 7,33) / 11 x 7 x 3 = (14 = x2) / 11 x 7 x 3 = 26,727272 = x3 = 6/π x 14.
Inversement, avec x1 = la coudée royale, on obtient (x1 = 7,33) / 3 / 7 x 11 = (3,8412698 = x-2) / 3 / 7 x 11 = (2,0120937 = x-3)
La progression constante est 6/π vers la limite supérieure et π/6 vers la limite inférieure.
6/π = 1,909090 et π/6 = 0,5238095, soit la longueur en mètre de la coudée royale.
Connaissant la relation continue entre la longueur du diamètre d’un cercle et la longueur de l’arc mesurant le tiers du demi-périmètre, reste à établir la relation entre la longueur de la coudée et la hauteur de 6/7ème le rayon du cercle. Cette proportion est de 12/((π/9) x 21) = 1,636363. Donc, la hauteur de 6/7ème divisé par 6, multiplié par 11 que l’on divise par 3, donne la longueur de la coudée. Inversement, la longueur de la coudée multipliée par 3, divisée par 11 que l’on multiplie par 6, donne la hauteur de 6/7ème le rayon du cercle.
En faisant la combinaison de ces deux relations proportionnelles entre la coudée et le rayon d’un cercle, on peut également écrire 6 x (6/π) = 11,45, que l’on divise par 7 = 1,636363. La fraction de ces deux décimaux est (6/π)/1,636363 = 1,166666 = 14/12 soit 7/6. Leur équation la plus simple est (6/π) x (7π/36) = 7/6 et (36/7π) x (π/6) = 6/7.
L’ensemble de ces proportions, lorsqu’on les dessine, permettent de vérifier la progression des deux suites précédentes. Lorsque l’on dessine un cercle de rayon 7, le tiers d’un quart de cercle mesure 3,66. Cette valeur multipliée par deux se reporte six fois sur le périmètre complet. Lorsque l’on multiplie 7 à (12/((π/9) x 21) = 1,636363), on obtient la longueur du rayon d’un cercle égal à 11,45. Cette valeur est (π/3) fois plus petite que 12 et la longueur de l’arc d’un tiers le quart de périmètre mesure 6, plus grand de 1,636363 fois que la coudée.
Lorsque l’on reprend le cercle de rayon 7, le tiers du quart de périmètre mesure 3,66, soit une proportion (6/π = 1,909090) fois inférieure. Si l’on multiplie 7 par 6/π, on obtient 13,36 de rayon pour le cercle de périmètre 84. Le tiers du quart de ce cercle mesure 7 et chaque arc de cercle compris entre les sommets de l’hexagone mesure 14 dans la proportion de π/3 supérieure au rayon du cercle.
Connaissant le rayon d’un cercle, on peut donc dessiner la translation permettant de reporter la mesure du rayon sur le périmètre d’un autre cercle dont la valeur de l’arc est celle du rayon donné.

Pour construire un cercle sur lequel on veut pouvoir mesurer une unité donnée suivant un nombre différent de mesures, il suffit de diviser le rayon du cercle dont on connaît la mesure en 11 unités plus petites que l’on multiplie par 7 et le nombre de mesures souhaitées sur le périmètre du cercle voulu. Si au lieu de reporter 12 fois la mesure de 5 sur le périmètre du cercle de rayon 9,545454, on avait voulu reporter 20 fois la mesure de 5, il aurait suffi de diviser 5 par 11, puis multiplier l’unité par 7 et 5 afin d’obtenir la longueur du rayon du cercle. Celui-ci mesure 15,909090, son périmètre mesure 100 et le quart de périmètre 25. Chaque unité portée sur le périmètre du cercle ayant une longueur de 1 centimètre, le périmètre du cercle mesure 1 mètre.
Cette géométrie, sans doute inconnue de l’Antiquité de Khéops détermine pourtant les fonctions usuelles du cercle telles qu’apparues avec l’utilisation de la roue. Permettant de transporter, elle servît également à compter dans le temps ou dans l’espace chaque mesure par son périmètre dont la juste mesure, mise en mouvement, détermine l’unité cyclique qui multiplie le nombre 1. De 0 à cet entier, toutes les unités du cercle sont comme autant de décimales quantifiables dans les proportions du cercle dont l’unité fait sept mesures.
L’ensemble des valeurs et proportions ici énumérées permettent de mieux apprécier la valeur des nombres usuels que nous retrouverons ensuite. La coudée royale, qui fait valeur d’unité est l’invariable qui définit la proportion de π. Elle correspond à 22/(7 x 6 ) dont l’écriture la plus simple est 11/21, facilité de propriété appartenant à cette pyramide, permettant de réduire tous les rationnels en l’écriture de quelques nombres facilement mémorisables. Ce langage mathématique définit un raisonnement de l’unité entière seulement portée par mesures. Irréductible, elle permet de parler couramment en “nombres pyramide” qui nous l’imaginons, durent faciliter tous les travaux de chantier.
S’il est facile de parler des proportions de la géométrie de Khéops, il faut toutefois en comprendre la valeur expérimentale, lorsque mis en pratique, le dessin impose des précisions de rigueur. La division d’une droite de longueur déterminée en unités plus petites de quantité impaire nécessite un dessin pour qu’elles soient égales. L’opération consiste à multiplier une longueur unitaire en autant de divisions voulues pour que les fuyantes passant en chaque mesure, recoupe la droite en nombres d’unités voulues.

En considérant la valeur d’une règle de 157,14286 pour la base et 200 pour la hauteur, l’ensemble des proportions de 11 et 14 sont reportées sur le dessin de deux règles par lesquelles les fuyantes déterminent chaque projection sur la règle de longueur 157,14286 par 200. Ainsi, on obtient deux unités de mesure qui permettent d’établir les rapports suivant:
Le demi-périmètre du cercle de rayon 50 est égal à 157,14286, soit la longueur de la base.
Le quart de périmètre du cercle de rayon 100 est égal à 157,14286, soit la longueur de la base.
Le quart de périmètre du cercle de rayon 7 unités est divisé en 11 unités égales à la longueur de la base.
Le 8ème de périmètre du cercle de rayon 200 est égal à 157,14286.
Le 7ème de périmètre du quart de cercle de rayon 14 unités est égal à la valeur de π soit 3,14285714. Dans cette proportion, π est 50 fois plus petit que 157,14286.
L’ensemble des relations comparables entre différentes proportions d’une même règle permettent d’établir une échelle, des translations, des régulations ou définir par le dessin des valeurs unitaires qui puissent être mesurées.
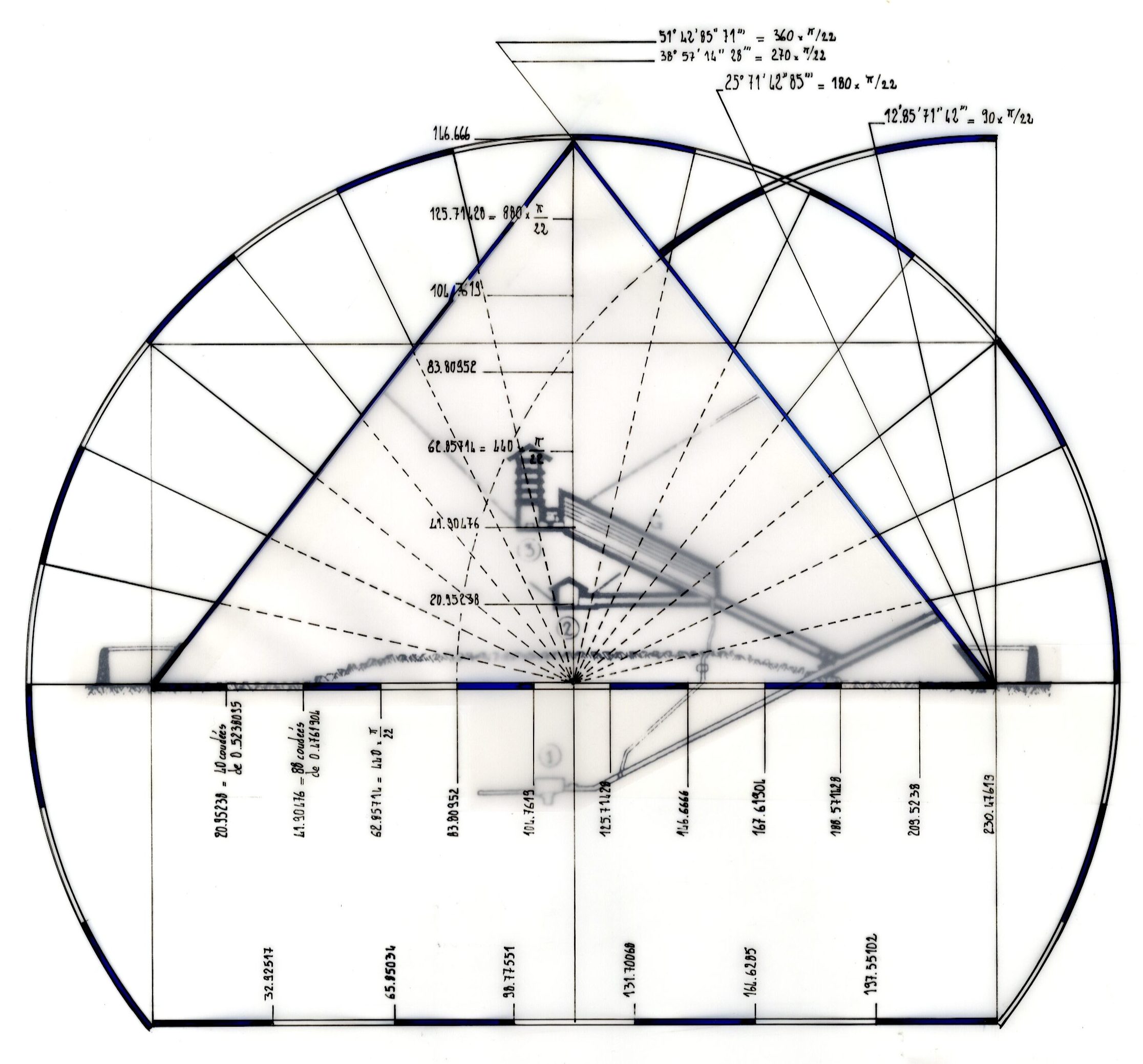
Lorsque l’on dessine le cercle de rayon 14 et que l’on reporte les sept proportions de longueur π sur chaque quart de rayon, on obtient la division parfaite d’un heptagone dont la projection verticale de l’extrémité de la base de la pyramide coupe le cercle sur la troisième unité de π. La mesure des quatre unités restantes se reporte sept fois sur tout le périmètre du cercle. Cela revient à dire que l’angle de la pyramide est 7 fois plus petit que 360, soit 51° 42′ 85” 71″‘ et que, dans la proportion de ce dessin,
cos de (90 – 51,428571) par 14 est égal à 11.

Page 190 de son ouvrage, J.Ph Lauer exprime la proportion de 4 fois la longueur du côté de la pyramide divisée par deux fois la hauteur à laquelle il résulte π en résultat de la fraction.
4 x 440 = 1760 divisé par 280 x 2 = 1760/ 560 = 3,14285714
En considérant que la hauteur vaut 14, le périmètre du cercle de rayon 14 est 88 avec π = 3,14285714. La valeur π est contenue 7 fois dans la longueur de la base, donc 88 divisé par 4 puis par 7 est égal à π, l’opération étant celle inverse du premier calcul. Cela revient à dire que la longueur de la base de la pyramide est 7π contenue 4 fois dans le périmètre du cercle, donc que la hauteur est de longueur le rayon. Quatre fois π est la proportion par laquelle on compte chaque mesure portée sur le cercle pour le diviser sept fois dans chaque quart de cercle. La valeur approchée de la hauteur sur la demi-base est 4/π = 1,272727.

On ne peut qu’être admiratif face à l’ensemble de ces résultats proportionnés de “telle sorte que ce monument unique au monde est bien la consécration matérielle d’une valeur importante pour laquelle l’esprit humain a dépensé des efforts inimaginables…“.
Cette citation de l’abbé Moreux dans l’ouvrage de J.Ph Lauer énonçait toutes les valeurs géométriques de la pyramide que le dessin de sa géométrie permet de démontrer sur une valeur différente de π, mais dans toute la perfection que le nombre exprime. Ce nombre, tel que nous le connaissons, est une valeur approchée par laquelle il devient possible de calculer toutes les mesures d’un cercle. Mais la valeur métrique qu’il exprime sur la quantité du nombre 1 est différemment concevable dans la géométrie de la pyramide. La valeur de π telle que conçue par le dessin n’est pas proportionnelle au rayon dans un demi cercle, mais un quart de cercle seulement que l’on reproduit quatre fois sur le périmètre. Cette valeur est 1,57142857 d’un rayon de sept unités qui font 14 pour le diamètre. Onze unités comptées sur la base de 14 et 7 donne la valeur de π par laquelle le cercle est mesuré.
Chaque unité est une division des nombres de la géométrie, exprimés par 7, 11 et 14. Lorsque l’on convertit ces nombres dans l’expression de π, le dessin de l’hexagone qui en réduplique le rayon résout l’équation à la valeur de π = 3,14285714 pour le périmètre d’un demi-cercle, mais sans exprimer chacune des parties autres que celles obtenues par le rayon.
Hors, la géométrie de la pyramide ne fonde le dessin du cercle sur aucune logique immédiate du rayon reporté trois fois pour en déterminer la valeur de π. Cette valeur est de moitié évaluée aux onze unités comptées sur un rayon en comprenant sept, et cette valeur multipliée “x” fois dans les proportions de la pyramide trouve en nombres métriques l’unité dans la coudée six fois plus petite que π dans la proportion du rayon. La hauteur de la pyramide est le rayon du cercle et le côté de sa base la longueur du quart de cercle dans lequel chaque unité est une valeur multiple de π reportée “x” fois, de la plus petite longueur à la plus grande.

Pour comprendre toute la valeur exprimée en chaque unité, la logique est celle du mètre dans lequel un est l’unité. Le cercle de rayon 1 mesure 6,28571428 de périmètre, le demi-cercle vaut π = 3,14285714 et le quart de cercle 1,57142857. Cette valeur est une proportion multipliée suivant l’échelle par le nombre des unités que la régulation de la pyramide permet de retrouver dans la valeur métrique de π et sa valeur en nombre d’unités. Pour cela, la logique est progressive est s’énumère en cinq séries de calculs fondés sur le dessin construit par les nombres 7, 11, 14 et 22.
La géométrie de la pyramide est composée sur la base de:
La valeur de π = 3,14285714
La valeur de π/2 = 1,57142857
La valeur de la coudée royale = π/6 = 0,5238095
La longueur de la pyramide = 440 coudées = 230,47619 mètres
La hauteur de la pyramide = 280 coudées = 146,66666 mètres.
* Si l’on divise la hauteur par deux, on obtient 73.33333 mètres qui font sept unités de 10,47619 mètres.
* Si l’on divise la hauteur par quatre, on obtient 36.66666 mètres qui font cinq unités de 7,33333 mètres.
* Si l’on divise la base de la pyramide par sept, on obtient une valeur de “π” pour les dessins n°11 et 12 égale à 32,925170 mètres, π fois plus grande que l’unité, c’est à dire 3,14285720 x 10,476190 mètres. Lorsque l’on divise chaque unité par π on obtient la mesure suivante de 3,33333 mètres. Cette mesure redivisée par π donne 1.060606 mètres que l’on redivise par π jusqu’à la plus petite unité de 0,337465 mètres.
Lorsque l’on fait le chemin inverse, chaque unité obtenue par la valeur de π est divisée par le nombre 7, de manière à calculer la plus petite unité d’un cercle que l’on multiplie ensuite par 11 pour la valeur d’un quart de cercle puis par deux pour le demi-périmètre. Le résultat est le suivant:
PREMIERE SERIE
| 0,3374655 / 7 = 0,0482093 | Unité contenue 4780,7413 ≈ 484 fois π² dans la largeur de la base. |
| 0,0482093 x 11 = 0,530303 | Unité contenue 434,6122 = 44 fois π² dans la largeur de la base. |
| 0,530302 x 2 = 1,060606 | Unité contenue 217,3063 = 22 fois π² dans la largeur de la base. |
| 1,060605 / 7 = 0,151515 | Unité contenue 1521,1444 = 484 fois π dans la largeur de la base. |
| 0,151515 x 11 = 1,66666 | Unité contenue 138,285720 = 44 fois π dans la largeur de la base. |
| 1,66666 x 2 = 3,33333 | Unité contenue 69,142863 = 22 fois π dans la largeur de la base |
| 3,33333 / 7 = 0,47619048 | Unité contenue 484 fois dans la largeur de la base. |
| 0,47619048 x 11 = 5,23809534 | Unité contenue 44 fois dans la largeur de la base. |
| 5,23809534 x 2 = 10,47619070 | Unité contenue 22 fois dans la largeur de la base. |
| 10,476190 / 7 = 1,49659867 | Unité contenue 154 fois dans la largeur de la base. |
| 1,49659867 x 11 = 16,462585 | Unité contenue 14 fois dans la largeur de la base. |
| 16,462585 x 2 = 32,925170 | Unité contenue 7 fois dans la largeur de la base. |
32,925170 x 7 = 230,476190
Partant de là, on redivise par 2 puis par 11 et l’on multiplie par 7 pour connaître la valeur de π contenue dans chaque unité. Le résultat est le suivant:
DEUXIEME SERIE
| 230,476195 / 2 = 115,238097 | Unité contenue 2 fois dans la largeur de la base. |
| 115,238097 / 11 = 10, 47619070 | Unité contenue 22 fois dans la largeur de la base. |
| 10,47619070 x 7 = 73,333334 | Unité contenue π fois dans la largeur de la base. |
| 73,333334 / 2 = 36,666667 | Unité contenue 2π fois dans la largeur de la base. |
| 36.666667 / 11 = 3,333333 | Unité contenue 22 π fois dans la largeur de la base. |
| 3,333333 x 7 = 23,333333 | Unité contenue π² fois dans la largeur de la base. |
| 23,333333 / 2 = 11,666666 | Unité contenue 2 π² fois dans la largeur de la base. |
| 11,666666 / 11 = 1,060606 | Unité contenue 22 π² fois dans la largeur de la base. |
| 1,060606 x 7 = 7,424242 | Unité contenue π3 fois dans la largeur de la base. |
| 7,424242 / 2 = 3,712121 | Unité contenue 2π3 fois dans la largeur de la base. |
| 3,712121 / 11 = 0,337465 | Unité contenue 22π3 fois dans la largeur de la base. |
| 0,337465 x 7 = 2,362259 | Unité contenue π4 fois dans la largeur de la base. |
| 2,362259 / 2 = 1,18112950 | Unité contenue 2π4 fois dans la largeur de la base. |
| 1,18112950 / 11 = 0,107375409 | Unité contenue 22π4 fois dans la largeur de la base. |
| 0,107375 x 7 = 0,751627 | Unité contenue π5 fois dans la largeur de la base. |
π = 3,14285720
π² = 9,87755138
π3 = 31,04373350
π4 = 97,56602130
π5 = 306,636072
Ces valeurs métriques sont celles concernant la longueur de la base de la pyramide. Lorsque l’on fait les mêmes calculs sur la hauteur, on obtient les résultats suivants:
TROISIEME SERIE
| 0,3374655 / 7 = 0,0482093 | Unité contenue 3042,29 fois = 968π = 88 x 11π = 7 x 44π² dans la hauteur de la pyramide. |
| 0,0482093 x 11 = 0,530303 | Unité contenue 276,57145 fois = 88π = 8 x 11π = 7 x 4π² dans la hauteur de la pyramide. |
| 0,530302 x 2 = 1,060606 | Unité contenue 138,285720 = 44π = 4 x 11π = 7 x 2π² dans la hauteur de la pyramide. |
| 1,060605 / 7 = 0,151515 | Unité contenue 968 fois = 88 x 11 = 7 x 44π dans la hauteur de la pyramide. |
| 0,151515 x 11 = 1,66666 | Unité contenue 88 fois = 8 x 11 = 7 x 4π dans la hauteur de la pyramide. |
| 1,66666 x 2 = 3,33333 | Unité contenue 44 fois = 4 x 11 = 7 x 2π dans la hauteur de la pyramide. |
| 3,33333 / 7 = 0,47619048 | Unité contenue 308 fois = 28 x 11 = 7 x 44 dans la hauteur de la pyramide. |
| 0,47619048 x 11 = 5,23809534 | Unité contenue 28 fois = 11 x 8/π = 4 x 7 dans la hauteur de la pyramide. |
| 5,23809534 x 2 = 10,47619070 | Unité contenue14 fois = 11 x 4/π = 2 x 7 dans la hauteur de la pyramide. |
| 10,476190 / 7 = 1,49659867 | Unité contenue 98 fois = 11 x 28/π = 7 x 14 dans la hauteur de la pyramide. |
| 1,49659867 x 11 = 16,462585 | Unité contenue 8,909091 fois = 28/π = 7 x 4/π dans la hauteur de la pyramide. |
| 16,462585 x 2 = 32,925170 | Unité contenue 4,454545 fois = 14/π = 7 x 2/π dans la hauteur de la pyramide. |
32,925170 x 14/π = 146,6666 mètres.
QUATRIEME SERIE
| 146,6666 / 2 = 73,333333 | Unité contenue 2 fois dans la hauteur de la pyramide. |
| 73,333334 / 11 = 6,666666 | Unité contenue 22 fois dans la hauteur de la pyramide. |
| 6,666666 x 7 = 46,666666 | Unité contenue π fois dans la hauteur de la pyramide. |
| 46,666666 / 2 = 23,333333 | Unité contenue 2π fois dans la hauteur de la pyramide. |
| 23,333332 / 11 = 2,121212 | Unité contenue 22π fois dans la hauteur de la pyramide. |
| 2,121212 x 7 = 14,848484 | Unité contenue π² fois dans la hauteur de la pyramide. |
| 14,848484 / 2 = 7,424242 | Unité contenue 2π² fois dans la hauteur de la pyramide. |
| 7,424242 / 11 = 0,6749311 | Unité contenue 22 π² fois dans la hauteur de la pyramide. |
| 0,6749311 x 7 = 4,7245177 | Unité contenue π3 fois dans la hauteur de la pyramide. |
| 4,7245177 / 2 = 2,3622588 | Unité contenue 2π3 fois dans la hauteur de la pyramide. |
| 2,3622588 / 11 = 0,2147508 | Unité contenue 22π3 fois dans la hauteur de la pyramide. |
| 0,2147508 x 7 = 1,5032556 | Unité contenue π4 fois dans la hauteur de la pyramide. |
| 1,5032556 / 2 = 0,7516278 | Unité contenue 2π4 fois dans la hauteur de la pyramide. |
| 0,7516278 / 11 = 0,0683298 | Unité contenue 22π4 fois dans la hauteur de la pyramide. |
| 0,0683298 x 7 = 0,4783086 | Unité contenue π5 fois dans la hauteur de la pyramide. |
Cette unité la plus petite de la quatrième série ne divise pas la longueur de la base de la pyramide en un nombre entier. Les valeurs de π qui multiplient chaques unités obtenues dans les résultats précédents sont celles exprimant la valeur unitaire de π dans la proportion du rayon et du demi-cercle lorsque π représente une longueur 3,14285714 fois plus grande que l’unité 1.
CINQUIEME SERIE
| 230,476195 / 2 = 115,238097 | Unité contenue 1,2727274 fois ≈ 4/π dans la hauteur de la pyramide. |
| 115,238097 / 11 = 10, 47619070 | Unité contenue 14 fois = 2 x 7 dans la hauteur de la pyramide. |
| 10,47619070 x 7 = 73,333334 | Unité contenue 2 fois dans la hauteur de la pyramide. |
| 73,333334 / 2 = 36,666667 | Unité contenue 4 fois dans la hauteur de la pyramide. |
| 36.666667 / 11 = 3,333333 | Unité contenue 44 fois dans la hauteur de la pyramide. |
| 3,333333 x 7 = 23,333333 | Unité contenue 6,2857153 fois = 2π dans la hauteur de la pyramide. |
| 23,333333 / 2 = 11,666666 | Unité contenue 12,57143 fois = 4 π dans la hauteur de la pyramide. |
| 11,666666 / 11 = 1,060606 | Unité contenue 19,755104 fois = 44 π dans la hauteur de la pyramide. |
| 1,060606 x 7 = 7,424242 | Unité contenue 19,755104 fois = 2π² dans la hauteur de la pyramide. |
| 7,424242 / 2 = 3,712121 | Unité contenue 39,510207 fois = 4π² dans la hauteur de la pyramide. |
| 3,712121 / 11 = 0,337465 | Unité contenue 434,61298 fois = 44π² dans la hauteur de la pyramide. |
| 0,337465 x 7 = 2,362259 | Unité contenue 62,087463 fois = 2π3 dans la hauteur de la pyramide. |
| 2,362259 / 2 = 1,18112950 | Unité contenue 124,17493 fois = 4π3 dans la hauteur de la pyramide. |
| 1,18112950 / 11 = 0,107375409 | Unité contenue 1365,92 fois = 44π3 dans la hauteur de la pyramide. |
| 0,107375 x 7 = 0,751627 | Unité contenue 195,13225 fois = 2π4 dans la hauteur de la pyramide. |
Il résulte de ces cinq séries une logique avant tout de l’espace qui enveloppe dans chaque mesure les unités qui doivent être comptées pour dérouler le cercle de diamètre la base, développer en hauteur toutes les proportions du rayon d’un autre cercle de diamètre plus grand dont le quart de périmètre fait onze unités. Ces unités sont le premier diamètre du cercle inscrit dans les fondations dont les mesures proportionnées sont unités de l’élévation.
La coudée royale, dont la valeur π/6 a servi aux dessins, se trouve dans la mesure de 5,23809534 mètres (première et troisième séries) , dix fois plus grande que la coudée telle qu’indiquée dans les proportions et onze fois plus grande que l’unité de 0,47619048 mètres contenue 484 fois dans la longueur de la base est 308 fois dans la hauteur. Ces deux proportions sont multiples de onze par 44 et 28. La valeur 11 fois plus petite que cette longueur de 0,47619048 est de 4,329 centimètres. Celle de 4,82093 centimètres (première série) est ≈π² plus petite que 0,47619048 mètres.
La coudée royale, dix fois plus petite que le nombre contenu dans les proportions de la pyramide est sans aucun doute la vraie valeur du bâti car seul grandeur applicable à l’échelle d’une construction aussi imposante pour être multipliée et divisée en unités qui puissent être comptées. La mesure de 5,23809534 mètres est comptée 44 fois dans la longueur de la base et 28 fois dans la hauteur, mais la proportion qui la divise ne peut être multiple de dix.
Les cinq séries de calculs établies d’après les dessins ont pour conclusion la valeur de π dans la perfection du nombre qui de mesures proportionnées sur les valeurs de 7 et 11 permet de définir la précision de l’unité. Un et deux sont des valeurs métrées qui n’ont d’autre arrondi que la mesure de π/2. 1,57142857 est la proportion de la pyramide lorsqu’on divise la longueur de la base par la hauteur. L’unité qui en résulte est celle de l’équation d’un cercle dans la hauteur dont le périmètre fait quatre côtés.
(2 x 440) / π détermine la hauteur et (π x 280) / 2 la longueur de chaque côté. La proportion de l’unité du triangle inscrit dans le cercle est 4/π et π/2, mesures par lesquelles la pyramide est dessinée dans le nombre des unités qui en déterminent l’équation pour toutes longueurs inscrites sur un cercle déroulé de la base jusqu’au sommet.
Nous avons vu dans le dessin n°2 que la valeur de π exprimée dans la pyramide de Khéops était égale à 44/14 pour le demi-périmètre et 44/28 pour le quart de cercle, ces deux valeurs étant respectivement π et π/2, mais par le nombre seulement, que la valeur de π exprime, différemment, dans la valeur du cercle complet. Le périmètre du cercle est 44/7 soit le nombre de fois que le rayon est reporté dans la proportion de π qui est onze fois une unité de sept.
1, 5, 7, 11, 14, 22, 28, 50, 70, 100, 140, 200, 220, 280, 440 sont les valeurs de l’échelle sur laquelle π est gradué en nombres de proportions et en longueurs métrées qui de jadis à nos jours ont pour seule unité la géométrie des lignes que le dessin peut tracer, de la plus petite valeur à celle définie la plus grande dans une pyramide qui ne compte plus les âges.