Lorsque pour faire suite au dessin du Bagua Xian koujue, j’ai recherché quel pouvait être le dessin des autres polygones, j’ai fait le calcul de la plupart des valeurs essentielles à leur identification. De la même manière que l’hexagone est composé de six angles réguliers, l’heptagone en compte sept de 51 degrés 42 minutes 85 secondes et 71 dixièmes. Cette valeur rappelée en mémoire, ramenait au souvenir de l’angle constant des pyramides de 51 degrés sur lesquelles de longues recherches ont déjà été menées. Mais voulant m’assurer de l’exactitude du nombre, j’ai ressorti le livre de J.Ph Lauer. Je ne l’ai relu qu’au moment d’écrire, après avoir construit la plupart des dessins, mais c’est en fouillant l’essentiel des chapitres que chaques questions sont venues s’imposer. Proportions, nombres compagnoniques et expression de π telle relatée par Archimède ont attisé la curiosité déjà vive du Bagua xian koujue, et l’aventure s’est poursuivie, sans doute pour être contée.
Oubliant les règles, j’ai pris pour seul outil le compas dont la promptitude établit les proportions, et de la première ligne régulée dans l’ordre des mesures, j’ai dessiné Khéops comme je l’imaginais. Aiguillée des informations essentielles, j’ai ressorti les rapports que les proportions indiquaient, cherchant la valeur juste aux approximations pour suivre par le calcul ma progression dans le dessin.
Les indications de l’ouvrage de J.Ph. Lauer arrêtaient la coudée royale à 0,524 mètres dans un rapport de proportions dont la base est de 440 et la hauteur 280 coudées pour les mesures de Khéops. Ces valeurs converties en mètres font une largeur de 230,47 mètres à la base pour une hauteur de 146,66 mètres, mais l’analyse étant de volonté dessinée, la géométrie en imposait l’oubli. C’est donc sur les mesures exprimées en coudées que l’ensemble des dessins ont pu être construits, dans la découverte progressive de proportions que l’ignorance a permis d’exprimer. Sans formation préalable en histoire de cette géométrie, j’ai dû faire les démonstrations de valeurs de loin connues, mais pour cela peu étudiées.
L’esprit, jeune de cette progression fouillée dans le tâtonnement de mes découvertes a permis de faire le jour sur des rapports inexplorés dont seule la valeur des nombres donnait l’idée de possibilités, qu’une longue recherche par le dessin a pu mettre en image. Usant des nombres qui ont légendes comme autant de questions posées, les démonstrations en font l’apogée jusqu’aux préceptes qui en ressortent, ce qui en fin d’ouvrage, résume les théories par toutes les certitudes affirmables dans ce qui suit.
π
est la valeur approchée du rapport du périmètre d’un cercle à son diamètre. L’objet de π est de permettre le calcul de la longueur d’un arc de cercle, proportionnellement au rayon qui le construit.
Quand on recherche la valeur de π la plus couramment appliquée aux calculs modernes, le nombre est pour la calculatrice de 3,14159265 correspondant à 1,04719755 fois la longueur du rayon reportée six fois sur toute la longueur du périmètre. Cette expression du nombre irrationnel fut assignée au début du XVIIIème siècle par le suisse Leonhard Euler, et l’on peut dire que ce ratio mit fin aux siècles de théories affirmées par ses devanciers.
La plus ancienne mention de π trouve expression en Grèce dans Les Eléments d’Euclide, fondateur de l’Ecole d’Alexandrie. La première lettre du mot grec περιμετρος signifiait alors une constante proportion du périmètre au diamètre du cercle, applicable au dessin de l’hexagone dont le ratio est de 3. Les variables exprimant le nombre prirent différemment des proportions suivant l’utilisation qui pouvaient être faites de l’expression dans le calcul des aires, des longueurs, des proportions, et celles exprimant une quadrature directe ou approchée.
En Egypte, le papyrus de Rhind évalue π à (4/3)4, Archimède en fixe la variable entre 3,10/71 < π < 3,1/7 , au IIIème siècle en Chine, Liu Hui utilise π = 3,14 et deux siècles plus tard, Tsu Chung-Chih mentionne π = 22/7 comme étant une valeur imprécise au bénéfice de π = 355/113 qu’il considère comme juste. A cette même époque en Inde, Aryabhatta obtient π = 3,1416 et plus tard, l’Europe du XVIème siècle verra Adriaen van Roomen revenir à π = 355/113.

En reprenant ces deux dessins pour les comparer aux mesures proportionnelles de la pyramide de Khéops, on obtient la valeur de “π” = 15,714286 pour un rayon de 50 et “π/2” = 11 pour un rayon de 70 unités de longueur. Ces deux valeurs expriment le ratio de l’unité du rayon reportée sur une portion du périmètre du cercle pour déterminer la valeur approchée de π. Avec un rayon de 50, le ratio est décimal. Avec un rayon de 70, le ratio est entier. Si le rayon du cercle avait mesuré 7, le quart de périmètre aurait été de 11, le demi-périmètre de 22 et le périmètre complet de 44.
Lorsque l’on reprend les proportions de Khéops citée dans l’ouvrage de J.Ph. Lauer, la fraction de 440 de la base sur 280 de la hauteur donne un résultat de 1,57142857. Cette valeur par deux est 3,14285714, expression supposée de π dans le dessin de la pyramide correspondant à la limite supérieure de π assignée par les calculs d’Archimède. La coudée royale est égale au tiers de π/2 soit une valeur proportionnelle de 0,523809523 correspondant à la longueur d’un arc de 1/6ème le cercle mesurant 0,50 de rayon (Dessin n°3).
Munis d’approximations moins relatives sur l’ensemble des mesures, la logique impose le raisonnement qui conduit de l’expression proportionnée la plus grande à l’unité la plus petite. De la coudée royale aux mesures de Khéops, 440 par 280 établissent des rapports réductibles par fractions jusqu’à l’expression la plus simple de 22/14, vingt fois plus petite que les premières. Le nombre π, dans cette relation est la longueur de la base sur la demi-hauteur soit 22/7. Similairement, la hauteur de la pyramide étant de 14, la demi-section de la base mesure 11 unités.

La hauteur de la pyramide mesure 14.
Le quart de périmètre du cercle de rayon 7 mesure 11 avec π/2=1,5714286.
Le quart de périmètre du cercle de rayon 14 mesure 22 avec π/2=1,5714286
Ces onze unités réparties dans la proportion de π/2 établissent les premières lignes d’un dessin dont la demi-section de la pyramide mesurerait 1,57142857 et la hauteur 2. Cette première échelle de valeur, pour être quantifiable dans les mesures de Khéops doit permettre d’exprimer pareillement une proportion rationnelle des mesures connues. L’échelle du dessin mesurant 1,57142857 par 2 représente l’unité triangulée contenue 140 fois dans la hauteur de Khéops et 140 fois dans la demi-longueur de la base, soit les proportions de la pyramide établies à l’échelle 1/140ème .
La règle du dessin, arrêtée suivant les mesures de 1,57142857 par 2 est donc identique à celles de 220 x 280, 110 x 140, 11 x 14, correspondant chacune aux dimensions de la demi-section de la pyramide. L’ensemble de ces valeurs, pour être aisément converties dans la suite du texte, sont représentées dans les tables de conversions qui accompagnent chaques pages. La première table convertit les unités courantes, la deuxième table exprime ces unités en mesures, la troisième table en énumère chaque nombre proportionné de la base et de la hauteur, la quatrième table en établit les conversions exprimées avec le nombre π, et la cinquième table traduit en mètres chaque unité d’un dixième Khéops.
TABLES DE CONVERSIONS
|
UNITES COURANTES |
Conversions |
|||||
|
Unites de la pyramide |
Proporsions par 14/11 |
Proportions par 28/44 |
Mètres de la règle de base 1,5714286 |
Mètres de la règle de base 157,14286 |
Mètres de la pyramide |
|
|
7 |
140 |
7 |
14 |
1 |
100 |
73,333 |
|
50 |
70 |
3,5 |
7 |
0,5 |
50 |
36,666 |
|
70 |
70 |
3,5 |
7 |
0,5 |
50 |
36,666 |
|
1/11 |
20 |
1 |
2 |
0,1428571 |
14,285715 |
10,476191 |
|
1/14 |
20 |
1 |
2 | 0,1428571 | 14,285715 | 10,476191 |
| 10 coudées | 10 | 0,25 | 0,5 | 0,0714285 | 7,1428573 | 5,2380953 |
| 20 coudées | 20 | 0,5 | 1 | 0,1428571 | 14,285715 | 10,476191 |
TAILLE DE LA PYRAMIDE |
B |
b |
h |
a |
c |
d |
|
Nombre de coudées |
440 |
220 |
280 |
356,08988 |
418,56899 |
311,12698 |
Coudée royale = 0,5238095= 1 unité. |
Suivant la proportion 440/280 = 1,5714286 |
314,28572 |
157,14286 |
200 |
254,34991 |
298,97785 |
222,23356 |
157,14286 = 300 fois la valeur de la coudée royale |
Echelle de la règle |
3,1428572 |
1,5714286 |
2 |
2,5434991 |
2,9897785 |
2,2223356 |
Le côté de la base mesure |
Mètres |
230,47619 |
115,2381 |
146,66667 |
186,52327 |
219,25043 |
162,97128 |
|
280 |
28 |
14 |
140 |
200 |
TABLE DES MESURES DE LA PYRAMIDE DE KHEOPS |
||||||||||||||||||||||||||
|
270 |
27 |
192,8571 |
|||||||||||||||||||||||||||||
|
260 |
26 |
13 |
130 |
185,7142 |
|||||||||||||||||||||||||||
|
250 |
25 |
178,5714 |
|||||||||||||||||||||||||||||
240 |
24 |
12 |
120 |
171,4285 |
|||||||||||||||||||||||||||
230 |
23 |
|
164,2857 |
||||||||||||||||||||||||||||
220 |
22 |
11 |
110 |
157,1428 |
220 |
11 |
157,1428 |
||||||||||||||||||||||||
210 |
21 |
150 |
210 |
150 |
|||||||||||||||||||||||||||
200 |
20 |
10 |
100 |
142,8571 |
200 |
10 |
142,8571 |
||||||||||||||||||||||||
190 |
19 |
135,7142 |
190 |
135,7142 |
|||||||||||||||||||||||||||
180 |
18 |
9 |
90 |
128,5714 |
180 |
9 |
128,5714 |
||||||||||||||||||||||||
170 |
17 |
121,4285 |
170 |
121,4285 |
|||||||||||||||||||||||||||
160 |
16 |
8 |
80 |
114,2857 |
160 |
8 |
114,2857 |
||||||||||||||||||||||||
150 |
15 |
107,1428 |
150 |
107,1428 |
|||||||||||||||||||||||||||
140 |
14 |
7 |
70 |
100 |
140 |
7 |
100 |
||||||||||||||||||||||||
130 |
13 |
92,8571 |
130 |
92,8571 |
|||||||||||||||||||||||||||
120 |
12 |
6 |
60 |
85,7142 |
120 |
6 |
85,7142 |
||||||||||||||||||||||||
110 |
11 |
78,5714 |
110 |
78,5714 |
|||||||||||||||||||||||||||
100 |
10 |
5 |
50 |
71,4285 |
100 |
5 |
71,4285 |
||||||||||||||||||||||||
90 |
9 |
64,2857 |
90 |
64,2857 |
|||||||||||||||||||||||||||
80 |
8 |
4 |
40 |
57,1428 |
80 |
4 |
57,1428 |
||||||||||||||||||||||||
70 |
7 |
50 |
70 |
50 |
|||||||||||||||||||||||||||
60 |
6 |
3 |
30 |
42,8571 |
60 |
3 |
42,8571 |
||||||||||||||||||||||||
50 |
5 |
35,7142 |
50 |
35,7142 |
|||||||||||||||||||||||||||
40 |
4 |
2 |
20 |
28,5714 |
40 |
2 |
28,5714 |
||||||||||||||||||||||||
30 |
3 |
21,4285 |
30 |
21,4285 |
|||||||||||||||||||||||||||
20 |
2 |
1 |
10 |
14,2857 |
20 |
1 |
14,2857 |
||||||||||||||||||||||||
10 |
1 |
7,1428 |
10 |
7,1428 |
|||||||||||||||||||||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
210 |
220 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
9,5 |
10 |
10,5 |
11 |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
110 |
0 |
/44= 0,7142857 |
/22 = 0,1428571 |
3/44= 0,214285 |
/11 = 0,285714 |
5/44 = 0,357142 |
3/22 = 0,428571 |
7/44= 0,5 |
2/11 = 0,57142857 |
9/44 = 0,64285714 |
5/22 0,7142857 |
/4 = 0,7857142 |
3/11 = 0,8571428 |
13/44 = 0,9285714 |
/= 7/22= 1 |
15/44 = 1,071428 |
4/11 = 1,14285714 |
17/44 = 1,2142857 |
9/22 = 1,2857142 |
19/44= 1,3571428 |
5/11 = 1,4285714 |
21/44 = 1,5 |
/2 = 1,5714285 |
TABLE DES MESURES METRIQUES
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
210 |
220 |
230 |
240 |
250 |
260 |
270 |
280 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
210 |
220 |
||||||
0 |
5,2380 |
10,4761 |
15,7142 |
20,9523 |
26,1904 |
31,4285 |
36,6666 |
41,9047 |
47,1428 |
52,3809 |
57,6190 |
62,8571 |
68,0952 |
73,3333 |
78,5714 |
83,8095 |
89,0476 |
94,2857 |
99,5238 |
104,7619 |
110 |
115,2381 |
120,4761 |
125,7142 |
130,9523 |
136,1904 |
141,4285 |
146,6666 |
La règle du dessin étant définie sur π/2, l’ensemble des régulations restent à devoir être exprimées. La valeur de π/2 résultant des proportions de la pyramide celles-ci sont réductibles à l’expression 22 x 14. Ces valeurs, pour trouver lieu de raisonnement dans le dessin du cercle doivent permettre d’en définir l’image du trait. Déroulé sur une ligne droite, un arc de 22 unités correspondrait au quart d’un cercle de rayon 14 unités. Inversement, le quart de cercle mesurant 22 unités, le périmètre complet serait de 88 qui dans la proportion d’un rayon de 14, représente la valeur de 2π.
Si nous reprenons l’expression du cercle de rayon 14 dont le périmètre est 88, la moitié serait 7 de rayon pour un périmètre de 44. La valeur de π/2 pour être égale au rapport du cercle, mesure par conséquent 11 unités pour un rayon de 7, soit 1 divisé sept fois pour un quart de cercle de longueur 1,57142857. La régulation de la pyramide correspond dans cette logique à π pour la longueur de la base et 2 pour la hauteur, soit la longueur du diamètre du cercle de rayon 1.

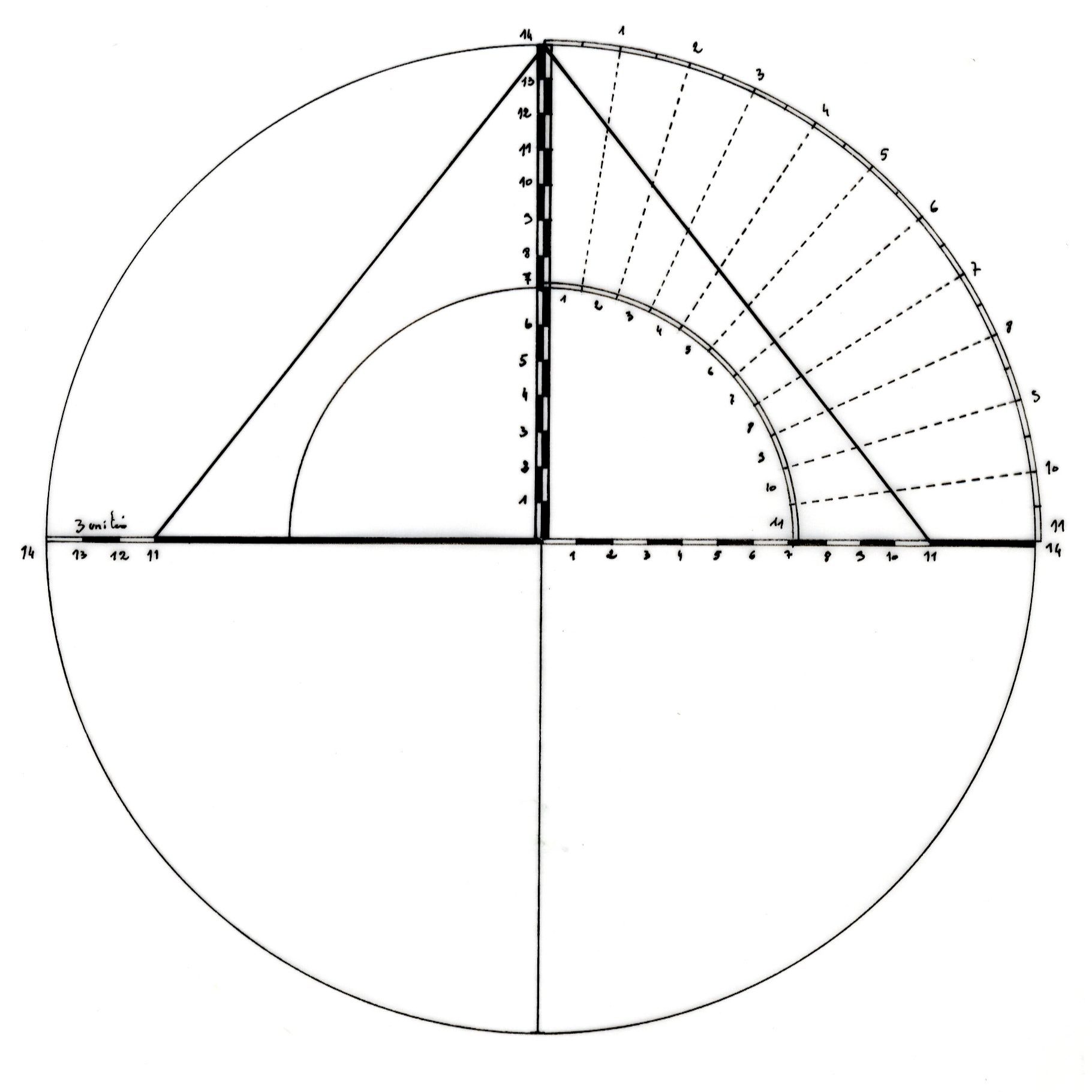
Le quart de périmètre du cercle de rayon 7 mesure 11 unités de longueur 1. A l'aide du compas, le quart de cercle peut être divisé en 3 arcs égaux, correspondant à la division de l'axe de longueur 11 en trois segments. Les 11 unités de l'axe étant de même longueur que les 11 unités du quart de cercle, les 3 segments dessinés sont de même longueur que les 3 portions d’arcs portées sur le cercle. Leur longueur équivaut à celle de la coudée royale, dans les proportions du dessin. Si le rayon du cercle avait mesuré 1, le quart de cercle aurait été de 1,57142857 et le tiers de cette longueur de 0,5238095. La valeur de 3,666666 représente la coudée à l’échelle du cercle de rayon 7, correspondant à la longueur de l’arc hexagonal d’un cercle de rayon 3,5. Cette valeur est celle obtenue par projection de la hauteur d’un arc de longueur 3,666666 sur la verticale du rayon du cercle. La longueur de chaque segment de l’hexagone mesure 3,5. La longueur de chaque arc de l’hexagone mesure 3,666666 dans la proportion de π/3. Si le rayon de ce cercle avait mesuré 0,50 mètre, la longueur de chaque arc aurait été de 0,5238095.En avertissement de la lecture qui suit, il n’y a donc aucun étonnement à voir les mesures tomber si juste. Elles n’expriment pour résultat que la valeur de nombres établis sur le fondement de proportions relatives au rayon d’un cercle égal à l’unité dont l’entier mesure 1. La logique en est fondée sur π dont la valeur constante retenue pour tous les calculs qui suivent est π = 3,14285714.
Tous les dessins, passés à l’encre, suivent l’ordre de progression par lequel mon raisonnement fut développé dans la logique de π comme interrogation essentielle expliquant l’architecture de Khéops. Des révisions, des questionnements se sont imposés au cours des pages pour mieux saisir la subtilité de l’oeuvre des pyramides. L’ensemble des calculs doivent bien sûr être vérifiés, en l’espoir qu’aucun ne contrefasse l’application suivie pour tenter d’exprimer par le nombre une forme, Merveille parmi les sept admirées du Monde Antique.