Khéops et le nombre d’or

     Vers 585 – 504 avant Jésus-Christ, Pythagore découvrait l’essentiel des théorèmes qui font la géométrie moderne d’aujourd’hui. Il fonda à Crotone une école de philosophie dans laquelle le nombre était considéré comme principe de toutes choses et il donna son origine au Nombre d’Or plus d’un millénaire avant que la Renaissance fasse un canon de cette proposition. Les siècles passés nomèrent le nombre par l’initiale de vingt-et-un, irronie de langage que le temps supporte dans le siècle nouveau qui nous parvient. Phidias est la proportion (√5+1)/2 d’un carré de base 1, double sur sa hauteur. L’écriture ϕ = 1,618 représente la quantité d’unités contenues dans la diagonale des deux carrés à l’intersection de la courbe du cercle dont le diamètre mesure 1. La récurrence de Phidias est constante par l’égalité de ((1/ϕ) + 1) = ϕ = (ϕ² – 1) = 1,618034.

     Dans le Mystère des Pyramides de J.Ph. Lauer, cette valeur de l’harmonie est exprimée par l’apothème dont la hauteur sur la demi-longueur de la base résoud la fraction par ϕ = 1,6185903. L’apothème mesurant √(308² + 242²) = 391,69886, la fraction par 242 résulte en l’expression de ϕ que les dessins suivants proposent de démontrer.

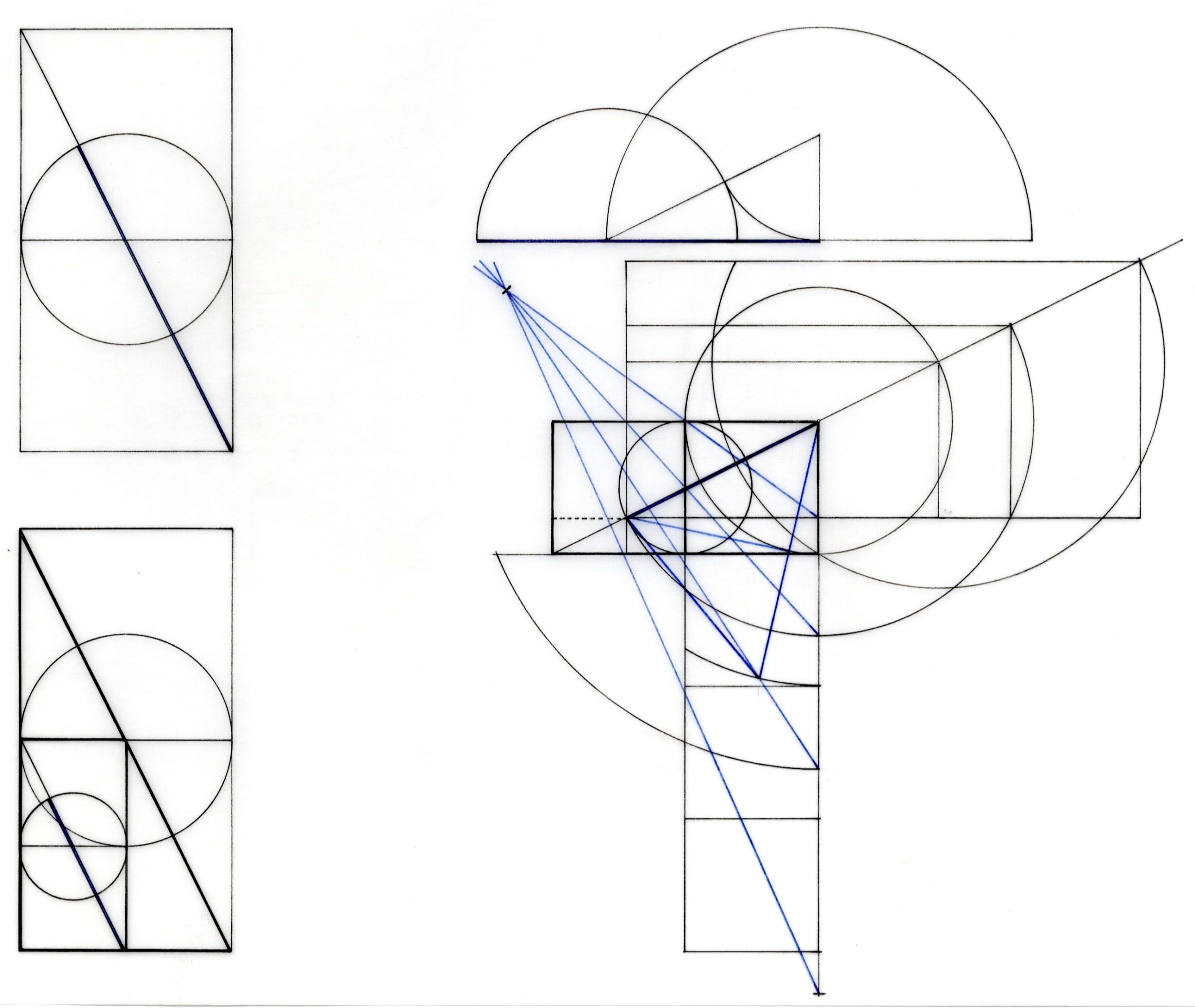
     Issu de la géométrie du carré et du cercle, le nombre d’or est une formulation du rapport qui résoud la fraction de l’apothème par la demi-longueur de la base de Khéops. Exprimé ainsi par le nombre qui conçoit l’harmonie décelée en cette géométrie, l’objet du dessin inverse la logique pour trouver dans le nombre les proportions qu’il contient. La récurrence de ϕ détermine une ligne par laquelle les fuyantes se coupent en un point d’où rayonnent les points de la géométrie aux intersections des courbes de l’unité 1.

     Replacé dans les justes proportions de Khéops, le quatrième dessin de la page précédente montre le rapport de 1 à ϕ par lequel exprimer la géométrie de Khéops. L’architecture que permet ainsi le dessin situe à cette échelle l’ensemble des points qui inscrivent les trois angles de la pyramide dans le cercle centré sur les régulations de ϕ. La droite passant par le centre du cercle trouve origine en ϕ² que la ligne oriente dans la direction similaire de la descenderie principale de Khéops. Cette magie semble-t-il impensable évoque la plus belle réalisation de l’esprit qui suggére avant Pythagore que Phidias ait été construit.

     S’il n’y a point volonté de convaincre l’importance est celle de montrer toutes les mesures d’une pyramide où le nombre fut ennoncé dans l’ampleur d’une époque qui parvint à traverser tous les rêves constructeurs dont l’harmonie est déïfiée. L’Egypte de Khéops fut l’ecole des génies par lesquels nous parviennent les plus vitales théories par lesquelles mettre en l’espace les mesures de la pensée qu’aux rois il appartient de définir par la coudée.

     Théâtre de toutes les Sciences qui essentielles nous sont parvenues pour exulter des valeurs de l’homme dans sa plus simple technologie, Khéops est dans le monde déesse des modernités parce qu’essentiellement créatrice des préceptes qui en font foi. Euclide, Archimède, Pythagore, tous en ont fait le pélerinage pour écrire en quelques nombres le langage d’une géométrie puissamment divinisée jusqu’à l’impossible contentement de voir par les sens toutes les valeurs d’un monument, que l’oeil mis à nu, n’absorbe que dans l’éloignement. Reflétée à l’imaginaire, Khéops dessine par l’invisible les sentiments de l’éphémère inscrits à la volonté.

Comprendre, tout ce qui a fait le monde de demain.

     Pour cela il faut démontrer, justifier par les mesures chaque valeur incalculable qui dans le nombre retient toute l’attention qu’il faut au rêve pour transporter en quelques lignes jusqu’au pinacle de l’entendement qui laisse quoi maître de sciences dans l’infini de cette clareté. Posée, elle s’énumère par les angles du dessin qui font aux géométries parfaite cohésion de dessein.

MESURE  DES  ANGLES

1 = 11°592176 2 = 13°74636 3 = 38°096413 4 = 26°565051 5 = 25°338536 6 = 64°661464 7 = 66°815648 8 = 75°027125 9 = 104°97288 10 = 38°157227 11 = 58°616636 12 = 48°359046 13 = 31°717474 14 = 16°641572 15 = 10°257590 16 = 42°975540 17 = 8°867233 18 = 128°15723 19 = 42°975540 20 = 52°820548 21 = 84°203912 22 = 107°38826 23 = 72°611736 24 = 95°796088 25 = 84°203912 26 = 19°791188 27 = 58°616636 28 = 78°407824 29 = 139°7494 30 = 40°250597 31 = 74°924097 32 = 63°434949 33 = 41°640954

L’ensemble de ces angles ont été calculés suivant l’inclinaison de l’apothème de 51° 84′ 27” 73 dixièmes. L’angle de la pyramide indiqué dans l’ouvrage de J.P Lauer est de 51° 50′ 35” et le dessin n°11 montre un angle de 51° 42′ 85 ” 71”’ correspondant au 1/7ème de 360 degrés.     Les variations indiquées par ces mesures sont celles résultant de la valeur de π différemment exprimée de la calculatrice au dessin. Le nombre enseigné par les écoles est de 3,14159265. Celui synonyme à 22/7 est de 3,14285714. La différence inscrite dans les décimales est de 0,0012644864 fois la longueur du rayon pour déterminer le périmètre du cercle. Cette variation, si infime soit-elle, produit les erreurs logarithmiques, qui confronte parfois la sensibilité au souhait de tout voir tomber juste. √(308² + 242²) x cos51,842773 = 242 √(308² + 242²) x sin51,842773 = 308 √(280² + 220²) x cos 51,5035 = 221,65414 √(280² + 220²) x sin 51,5035 = 278,69238 √(308² + 242²) x cos51,428571 = 244,22025 √(308² + 242²) x sin51,428571 = 306,2425

     Sur le dessin, la longueur AB = 14, la longueur AC = 11 et la longueur BC 14/√2. Toutefois, je n’ai pas su démontrer AC et BC ni par le calcul des angles, ni par le dessin.

     Le calcul de l’ensemble des angles s’est imposé par constation comparée du dessin n°21 à la coupe de la pyramide. L’inclinaison de la Grande Galerie est parallèle à la droite passant par ϕ² et le centre du cercle joignant les trois angles de la pyramide. L’angle de cette droite avec la base de la pyramide est de 23°18’43”52”’ sur le dessin. A la page 224 de son ouvrage, J.P. Lauer indique une inclinaison de 26°5 pour la descenderie, le couloir ascendant et la “grande galerie” de Khéops ce qui vérifie également le dessin suivant.

     On remarque également:

La jonction de la descenderie et du couloir ascendant marquée par le passage du cercle de rayon ϕ dont le centre est l’angle oposé de la pyramide. Ce cercle passe par le sommet, traverse le coude des deux couloir et marque sur l’horizontale un point d’intersection de longueur ϕ situé dans le prolongement de la descenderie Sud de la pyramide. 

Le puit souterrain est dans l’axe d’un côté du carré. 

La chambre de la Reine est située au centre du cercle passant par les points d’extrêmité de la pyramide. 

L’intersection de la projection verticale du sommet de la pyramide avec le cercle de rayon le côté du carré, détermine avec l’angle bas de la pyramide une droite passant au sommet de la chambre funéraire du Roi.

     Certains détails, s’ils sont remarquables auraient pu n’être que circonstanciers aux proportions d’ensemble de la pyramide. Tel est le cas du coude formé par les deux couloirs dont l’angle est situé sur un cercle passant au sommet. Toutes les autres observations sont, et seulement, la conséquence du dessin de deux carrés imbriqués d’un cercle où apparaît la pyramide.

     Dans la suite du dessin précédent, celui-ci oriente pareillement la pyramide mais à l’inverse de l’ensemble des régulations précédentes. Les pointillés indiquent par le graphisme ce que le discours ne peut qu’éluder malgré quelques détails qui se doivent être précisés.

     Le haut du couloir conduisant à la chambre de la Reine se trouve dans le prolongement horizontal du plan de la pyramide au point marquant l’un des angles du carré de construction. Cette droite marque les deux points de passage du couloir ascendant à la Grande Galerie. Le premier est celui défini par la projection verticale dans le plan de la pyramide du point d’intersection entre l’apothème est la fuyante en ϕ. Sur cette ligne se trouve également le puit situé à la base de la Grande Galerie jusqu’au coude déviant vers le Sud en dessous de la base.

Le puit souterrain se trouve sur la ligne horizontale du repère des deux carrés et l’extrêmité du couloir Sud s’arrête dans le prolongement de la verticale au plan de Khéops, à l’intersection de l’apothème avec le côté d’un des carré.

Enfin, la descenderie Nord du haut de la Grande Galerie est dans le prolongelent de ϕ², de même que chaque point situé au sommet des deux chambres funéraires.

     Aucune de ces régulations ne pouvait avoir d’autres dessins que celui de ϕ dans sa géométrie malgré la tentation de vouloir accuser la volonté qui parfois vient à prouver par excès chaque hypothèse. L’objet du dessin est celui de comprendre sans détermination à de faux principes qui n’auraient, à cette époque aucune justification de procédés.

     Pour comprendre ce que ces dessins invoquent de géométries, il faut par d’autres repères construire le nombre dans ses proportions. Celles de la pyramide sont indiquées pour expliquer ce qui d’ensemble permet de trouver toutes les inclinaisons des angles intérieurs qui régulent les aménagements des galeries et chambres sépulcrales par les valeurs de la récurrence qui vont de 1 à ϕ².

     Lorsque l’on dessine la section de la pyramide dans la proportion de 7 centimètres en hauteur, la longueur de la base mesure 11 et l’apothème 8,9022469. La hauteur divisée en 14 unités permet de tracer la droite passant par la sixième unité et l’intersection de la diagonale au quart de cercle de rayon 3,5. Cette droite, à la verticale de l’extrêmité de la base, détermine une hauteur qui divise par trois coudées la demi-base du triangle. La droite passante par l’intersection de la diagonale du repère au cercle de rayon 3,5 et l’intersection des deux diagonales d’un carré de hauteur la coudée détermine le centre du cercle exinscrit aux trois sommets.

     Pour trouver la valeur de ϕ, il faut ensuite tracer le cercle de rayon la demi-base, celui de rayon la longueur de l’apothème, et celui de longueur la largeur de la base dont le centre est l’une des extrêmités de la base. Connaissant la longueur de la demi-base, on trace le cercle de diamètre cette longueur dont le centre situé sur le même côté de la pyramide dessine la ligne passant au sommet. L’intersection du cercle de rayon la demi-base et celui dont cette longueur est le diamètre détermine un angle des deux carrés dont le côté passe au centre du cercle situé à l’extrêmité de la base du triangle. Pour construire les deux carrés, il faut tracer la perpendiculaire à ce côté passant par la centre du cercle et reporter en hauteur la longueur de la demi-base.

     La droite perpendiculaire passant au centre du cercle et le segment de base des carrés, coupe les cercles de rayon ϕ et 2 en chaque point de la construction. Lorsque l’on trace la droite passant par ϕ et le centre du cercle de diamètre la demi-base, l’orientation du point de fuite coupe le cercle de rayon la hauteur de la pyramide dont le centre est l’angle commun au deux carrés. La droite passant par ce point et la deuxième extrêmité de la base de la pyramide, coupe la droite d’inclinaison inférieure en la longueur de ϕ². La projection du sommet de la pyramide sur cette droite rejoint le point de fuite par l’angle opposé qui est commun aux deux carrés. Cette construction terminée permet des comparaisons aux régulations supposées autrement conçues avant qu’une conclusion n’exprime par logique ce qui ressort des dessins dans les proportions de ϕ.

     Les informations instruites par Le Mystère des Pyramides indiquent l’expression d’une valeur proche du nombre d’or que la transcendance la plus simple écrit par (√5 + 1)/2 = 1,618034. La fraction de l’apothème sur la longueur de la demi-base est supérieure à ce nombre de 0,0005563 décimales qui suposent un autre tracé que ceux dessinés précédemment.

     La logique la plus immédiate permettant d’obtenir la valeur de ϕ par le dessin, consisterait à dessiner les carrés et le cercle de longueur la demi-base, reporter sur la diagonale la hauteur de l’apothème, et suffire l’analyse par constatation que le rapport existe en “la proportion d’un carré surmonté d’un cercle dont la droite au centre et l’extrêmité du carré détermine la hauteur de la pyramide”.

     Si nulle conviction ne peut être tirée d’une constatation aussi simpliste, reste pourtant l’expression d’une valeur seulement affirmée par ce dessin qui pour trouver l’égalité du nombre, oblige le compas à faire rotation du segment de longueur ϕ dans le rapport de la demi-base = 1. Il résulte une logique différente du nombre ϕ que la variable de 0,0005563 résume en simplicité, et sans doute pour exprimer la géométrie de ϕ autrement dessinée par les proportions données.

ϕ = 1,6185903
1/ϕ = 0,6178215
ϕ² = 2,6198347

     Lorsque la hauteur de la pyramide mesure 14, la longueur de la base mesure 11 et la hauteur de l’apothème (11 x ϕ). Quand ϕ = 1,6185903, la récurrence de ce nombre n’existe pas, mais la valeur approchée détermine une relation qui dans la pyramide trouve des traductions par l’objet du nombre π dont la fraction 22/7 permet les conversions en valeurs approchées.

     Si l’on convertit ces proportions par celles de 440 pour la largeur de la base et 280 pour la hauteur, ϕ² est égal au quart de la base divisé en sept unités que l’on multiplie par 22 et que l’on redivise par 7. La racine carrée de cette mesure est multipliée par 7, puis divisée par 11, auquel on ajoute six unités de 440 pour obtenir la mesure d’un quart cette longueur égale au nombre de ϕ².

     Nul besoin de poursuivre une démonstration que le dessin par lui-même ne saurait contenir autrement que par simple logique d’une réalité de Phidias différente de ϕ. Ce nombre, égal à la longueur de l’apothème lorsque la base mesure 2 est inscrit dans le dessin du cercle par les proportions de la pyramide. La hauteur étant celle de 14 pour une largeur de 11 unités, 2 divisé par 11 donne la hauteur de 2,545454. Cette mesure est du double la valeur déjà observée de 4/π lorsque par cette hauteur la demi-base mesure 1.

     Reprenant tous les dessins, il est alors aisé de conclure par convertion de tous les nombres en ceux proportionnels à π. Le dessin de ϕ entre dans la composition de deux carrés dont les côtés et le diamètre du cercle imbriqué mesurent π. La base de la pyramide mesure 2π, l’apothème ((π√5 + π)/2) et la hauteur exacte 3,9977761. Si la valeur de π avait été de 3,1446055, la hauteur exacte serait celle de 4, la base celle de
2π et l’apothème celle constante de πϕ avec ϕ = (√5 + 1)/2.

     Si parfaitement inscrit dans le dessin du “triangle pyramidal”, le nombre d’or n’accepte cependant qu’une seule variable de π égale à 3,1446055 correspondant au cercle de périmètre 360 dont le rayon mesure 57,240884. Comparativement aux valeurs attribuées à π, 3,1446055 est 0,00301284 fois plus grand que le nombre indiqué par la calculatrice, et 0,0017483 fois plus grand que 22/7. Ces nombres variant suivant la typologie du dessin géométrique, la valeur de 3,1446055 n’est pas plus improbable que toutes les autres, à condition de fixer dans la logique du nombre une déontologie relative du carré et du cercle qui accepte par l’harmonie cette valeur supérieurement aux autres.

     Dans son ouvrage Le mystère des Pyramides, J.P. Lauer cite en note page 270 la relation entre π et ϕ telle que signalée par Paul Montel, membre de l’Académie des Sciences. Avec π = 3,1416, la valeur de 1/ ϕ = (π/4)² = 0,617, soit 1/ϕ à 1/1000ème près. Si nous comparons ce résultat à ceux précédemment observés, il semble certain qu’une relation plus effective puisse être exprimée avec π = 22/7, la valeur approchée de ϕ étant de 1,6185903 = (√(4² +π²))/ π. 

     Si, pour affiner le calcul, nous poursuivons dans la logique de tout ce qui précède, nous pouvons également affirmer que π = 3,14285714 est une valeur inférieure à celle de π telle qu’idéalement représentée par la ligne du cercle, et qu’en conséquence π = 3,1446055 représente le nombre proportionnel au rayon d’un cercle permettant l’harmonie du carré, du triangle et du cercle. Cette valeur supérieure à celle couramment employée dans les dessins d’architecture connait d’autres régulations que celles observées dans la géométrie de Khéops, mais qui, pour trouver fondements, doivent d’abord être étudiés.

     Comme les anciens héritiers du génie concepteur d’Imhotep, la nécessité de définir l’espace par des valeurs numériques implique qu’une volonté en exprime effectivement le besoin, moins sans doute pour le bienfait des Sciences que celui de vouloir chercher dans le dessin la juste expression des formes et de leur harmonie. Et peut-être, devrions-nous regretter le temps de cette importance qui dans l’esprit des hommes savait éveiller la créativité essentielle au maintient de l’évolution culturelle.

     L’Architecture est une Science des Arts qui en cela s’applique par l’esprit, pour passer en d’autres mains sous le regard de popularités, dont la sensibilité n’est atteinte que par l’invisible conformité à des valeurs conservatoires de l’habile créativité que l’artisan transmet dans la numération des formes. Les cannes de maîtres ne font pu la palme et les matières n’ont plus les patines d’autrefois. Le froid des villes envahit l’espace et la poésie n’a plus de mots.

     Il faut à cela des réformes, des décrets ou des révolutions. Il faut de la modernité dans le viscéral des conceptions, pour qu’essentiel reste l’esprit qui en gravite les motivations jusqu’à ces profondeurs les plus froides du jugement. Les caractères profanes des édiles en tous siècles ne font qu’éteindre les beautés de demain, par lesquelles l’espoir fait déjà vivre l’attention qui seule permet aux volontés de grandir. L’homme ne sait plus grandir que par son nombre ombilical sans regarder autour de lui ce qui le porte vraiment. Il se nourrit d’allégories joyeusement commandées, sans plus donner place d’honneur aux bienfaits de l’existance, ceux modestes, qui témoignent de volontés par goûts et couleurs mis en discernement.

     Les apparences, parfois, laissent s’affranchir les idées des plus grands phénomènes qui gravites dans l’histoire pour libérer de l’homme ses instincts sentencieux que les modernités transforment en imaginables talents. Les époques ont leurs légendes et les notre prennent fin par habitude déjà servile de l’espace inféodé à des rêves trop merveilleux pour ne pas tarir de l’humain qui parfois vient à manquer dans le dimensionnement du monde. Les rêves montent haut, et l’esprit reste bas dans l’auréole d’une sphère en totale inéquation de l’homme face au monde le plus immédiat de l’existance.

     Si les Sciences avaient été modernes, elles auraient su expliquer que le nombre est une clef d’or à celui qui en atteint la subtilité équipollente la plus essentielle. Il est nul besoin de créer des relativités si elles ne peuvent expliquer le nombre dans ce qu’il a de plus remarquable, par sa variabilité dans un espace en valence continuelle pour créer et inventer de nouveau, les semblables pôlarités d’un monde qui évolue. Les modernes d’autrefois ont certe l’avantage de cette évolution pour relater par renoncements tout ce qu’il fallut traverser de fins jusqu’à l’évidente nécessité du résultat, attesté aujourd’hui par ce qui est parvenu à prouver l’importance d’hypothèses consenties.

     Ces preuves, qui ont essentiellement traversé les siècles pour venir au monde par leur génèse, ont dû questionner la pensée avant que les modernes en admettent le fond par l’individuelle raison de façonner une humanité dont l’évolution du concept est conditionnelle du savoir. L’école a fondé l’universalité du nombre capable d’éveiller le fond sensible de chacun, par l’étude raisonnée de connaissances admises et construites au regard des pluralités. Coutumières de l’espace géomètre des arpents, les populations connaissent le nombre par son dessein de grandir par les ares les bienfaits de la terre, que les arts exhaussent de charmes imprévus. Impérissables, ils affrontent l’incohérence du temps pour transmettre par mystères l’éveil qu’ils suscitent en connaissances somptueuses venues d’outre temps.

     L’Antique a mis au monde toutes les philosophies qu’il fallait à l’homme pour faire source à l’évolution espérée, en regain des transformations possibles qui de l’homme en son être fait place au renouveau. Plus beau, plus grand, plus juste dirait-on, et sans doute moins servile du caractère difficile qui met à condition les valeurs en chacun, cultivées par volonté d’exister par le monde comme aucun n’imaginerait faire oeuvre de son temps. C’est sans doute en cela que Khéops est un mystère essentiel au devenir du savoir souverrain que l’humanité travaillée de morales doctrinaires met en balance de pratiques justifiables autrement.

     On ne peut voir Khéops sans se laisser balancer dans le vide immense qui nourrit de questions, l’inquiétude d’être au pied infini d’une montagne que l’homme a dressée par la force du repos. Celui éternel d’un roi de mille âges qui oeuvra en son art à l’unification de courants et de castes de latitudes inverses pour bâtir dans le sable l’inusable fronton. Pyramide par l’ampleur du pas promené au quatres faces de ses fondations, pyramide par le coeur de chemins emmenés aux tréfonds de l’élévation, pyramide par couleurs enlevées de la cîme pour éteindre ses graduations, pyramide de douceur reflétant l’harmonie du soleil dans sa carnation.

     La géométrie ne peut effacer cela, ni par le nombre ni la phobie de voir en ce monument la preuve impartiale de tyranies, empreintes à ces rois par démonstration de l’esprit qui voulait en ces temps rejoindre la terre. Sans mourrir vraiment et sans perdre le souffle qu’il fallut à ces rois pour inspirer aux mondes tant de finesse et tant de beautés, tant de juste existance aux peuples qui ont fait vies de servilités dont la mémoire est par l’Egypte, l’histoire de toute l’Antiquité.

     Il y a dans ce mystère une incommensurable injustice qui veut que Pharaon soit de taille au gigantisme, pour contraintre par le sang ce qui nourrit le muscle et soumettre à son instant les vies d’autres générations. La force d’un homme a toujours besoin de chèvres pour porter toutes les chandelles qui éclairent son campement, mais a cela il faut également l’esprit pour savoir encore tirer profit des mains alertes qui tiennent son ouvrage. Pharaonique sans doute, et bien plus qu’un roi ne saurait penser faire cruauté en ce monde pour mettre au coeur les proportions, justement capables d’entreprendre à raison l’évolution de tout un pays.

     Savoir, compter, mesurer, connaître. Le nombre est en π plus qu’un symbole altesse de toutes les théories qui ont pu être fondées. C’est un simple élément de dessein par le cercle pour donner à savoir tout ce qui peut être fait. Plus juste sans doute que l’irrationnel attribution d’un ratio potentiel pour compter les mesures, le nombre élevé par l’unité première est fraction discernable en chaque entendement. Cette magie, sans doute, fit l’unité entière de nômes asservis à la féérie des lieux, où l’honneur en arme par usure de la pierre met en fait plus de paix que d’interminables conflits.

     L’eau, le pain et l’ombre d’un soleil pour assurer bienveillance au peuple pharaon dont les arts culminent par l’évidente sincérité qui devait unir l’engeance au souverrain. Dénudé, presque, et sans armes pour défaire l’alliance qui trône au côté de son roi, homme et femme sans loi de principe pour éteindre par force cette humanité, dont la candeur du feu est d’ardeur ancestrale pour avoir créé la part de l’homme. La vie est en tout l’éternelle beauté que ce monde su transmettre de son essentiel fondement, et tout en cela reflète l’apogée d’un monde contruit sur des valeurs humaines. La médecine, la géométrie, l’art d’établir de grands chantiers, employant autant de bras que la puissance pharaonique pouvait en rayonner jusqu’aux fondations. Celles des humbles qu’on imagine sains, vifs d’esprit et habile à l’oeuvre, sans l’animausité qui est au sphinx la part féline de la virilité de l’homme. L’harmonie ainsi mise en relief est seulement celle d’un paysage, celui peint par toutes les fresques qui font légendes jusqu’au delta.

     On ne peut contempler Khéops sans être sensible à cette réalisation d’un nombre comme celui de Meïdoun, unique dans un état, dont le fondement essentiellement construit fut plus qu’instance géométrale pour assembler en cette Vallée les éléments d’une géométrie. Les tyrannies eurent leur époque mais moins sans doute en ce temps là qui du meilleur fruit des nômes dépassait en travaux surhumains, l’insoumission de pauvres âmes pour faire cloisons d’oeuvres bâties dont l’édifice est seule raison de progresser par l’esprit . La pureté massive de Khéops est une somme d’arts à bout de bras, portés jusqu’aux plus humbles pour le bienfait des plus grands, mais sans les distinctions de castes employées jusqu’au tombeau.

     Souverain par les Dieux qui affrontèrent le néant, Pharaon est l’Horus du corps egyptien, unifié par les masses lapidaires d’un libage embaumé du suint de l’ingéniosité. Jamais souverain ne ferait par le nombre serviles éclats de sa royauté pour promettre au dédain la mort dont il sait pouvoir déjà être béatifié. Panthéon dioscurien du Nil éternel, la pyramide est un embaumement de la foi artisane des sables pyrogènes consacrée à l’oeuvre d’un monument. Ces peuples portaient sobrement l’honneur de peindre autrement leur paysage, par force d’éfforts pharaoniques pour lever sous le ciel une montagne.

     L’Osirisme de cette époque avait pour coeur un oiseau, trop libre pour s’éteindre du nantissement macabre qui disperça le feu de par tout le pays, et fit vent de la terrible flamme qui par la mort crevait en lui. L’oiseau prit le sable dépouillé de la braise, et mit suint de cinname pour calmer sa douleur. Il prit le flambeau purifié de la vesse et mit au vol l’aube au pays. Traversant le soleil jusqu’à s’y peindre il leva le secret qu’il avait de la vie, jusqu’à faire feu d’un horizon de laizes qui prit de l’âme son énergie. L’ammos amert fit π du feu, et l’oiseau s’envola.

     Il y a depuis ce monde des encres qui ont coulé en flots bien plus serviles de l’incertitude des nombres, passés de pierres à doutes sur l’origine finale de locutions fondées en théorèmes construits. Nil admirari fut le plus juste épiphonème qui justifia la pensée des sages successeurs, d’un temps où l’imparti traduisait la connaissance de dessins instruits par l’ampleur du propos. Sans tables pour faire lois des traits imagés de l’espace, la seule géométrie est celle de constructions, équivoques dans la forme pour cheminer par l’édifice jusqu’au fond d’inventions secrètes dans leur plan.

     Il eut fallu vingt siècles pour atteindre par le dessin les formes singulières qui ont bâties Khéops. Vingt siècles de questionnements pour traduire en graphèmes les nombres inscrits dans l’ombre de quatre lignes, élevées par l’aire d’un cercle accompli. Les nombres d’entière signifiance de l’unité indiquent par mesures signifiées de l’entité l’idéale harmonie de la courbe déployée qui de l’être noma la divine proportion. Oeuvre composée de tous les savoirs pratiques il n’y eu de postérité que sous la Grèce Antique qui énonça par termes les syllepses graphiques qui annoncèrent tous les fondements des mathématiques appliquées.

     Le nombre qui par là, ennui le moderne, est fait de cet or que les siècles d’expériences ont combinés aux figures abstraites de l’existance pour créer l’harmonie. Si la valeur égyptienne de l’initiale d’un cercle n’avait eut la juste equité de son nombre, peut-être aurions hérité des constantes qui du cercle au carré font logique affirmée. Mais pauvres démunis de mystères topiques, nous ne serions plus que les baladins, chantant de maximes l’éloge des princes qui jadis inventèrent la sublime beauté, du nombre fondateur d’une architecture que le temps n’éprouve que pour être sublimé.

     Les dessins, qui jusqu’ici ont permis de démontrer les particularités essenrielles de la géométrie de Khéops, étaient principalement attachés à la coupe triangulée de la pyramide permettant de voir en vraie grandeur les proportions de son élévation.. Ces proportions puisées dans le l’ouvrage de J.P. Lauer étaient de 440 par 280 coudées, devenues 484 x 308 pour parfaire les calculs jusqu’à l’unité d’une coudée de 0,47619048 mètres.

     Cependant, la face triangulée de la coupe médiane de Khéops ne permet pas toutes les démonstrations, et pour parfaire le nombre par ce qu’il a de visible, le dessin doit pouvoir se poursuivre par les parement extérieurs de la pyramide. Tous quatres égaux entre eux une face seulement suffit à l’étude de ce qui suit, bien que nombre de questions attendent dessins pour parfaire l’analyse d’un plus vaste énoncé.

     L’objet de tous ces questionnement vise essentiellement à comprendre par le dessin les modes de calcul qui pouvaient exister pour permettre au nombre d’approcher ceux connus des contemporains. Les valeurs de π et de ϕ sont des formulations de l’espace qui certe ont eu un renouveau mais sur le fondement de valeurs plus anciennes. Les dessins qui suivent cherchent à montrer comment cette origine des nombres à pu trouver ses fondements en Egypte pour susciter plus tard en Grèce, toutes les études mathémathiques parvenues à faire école.

LES SEPT ANGLES DE LA PYRAMIDE

a = 51°84’27”73”’
b = 38°15’72”27”’
c = 58°29’13”34”’
d = 31°70’86”66”’
e = 41°98’57”59”’
f = 48°01’42”41”’
g = 45°

Avec a = 360/7, on obtient:
a = 51°42’85”71”’
b = 38°57’14”29”’
Les autres angles ne peuvent être calculés que par la trigonométrie, et sans calculatrice, ce qui nécessite une longue réfléxion. Mais quand on compare ces valeurs à celles d’un triangle inscrit dans un cercle de rayon 60, on obtient:
a = 60
b = 37,069293
h = 47,1791
c = 22,930707
d = 52,456504

Avec un cercle de rayon 57,272726
a = 57,272726
b = 35,384324
h = 45,034594
c = 21,888402
d = 50,072116

L’angle de 51°42’85”71 correspond donc à un cercle de rayon 58,824245.
a = 58,824245
b = 36,342886
h = 46,254582
c = 22,481359
d = 51,42857
Lorsque l’on fait cos 51,428571 on obtient 0,6234898.
Lorsque l’on fait sin 51,428571, on obtient 0,7818314
0,7818314 / 14 x 11 = 0,6142961.
Là, plus rien ne marche.
La valeur de π étant différente de celle habituelle de 3,1415927, toutes les valeurs trigonométriques sont changées.
0,6234898 x 58,824245 = 36,676317
0,7818314 x 58,824245 = 45,990642
Et pourtant, tous les calculs précédents sur la valeur de π = 3,14285720 tombaient justes, au millième près.

     Les proportions connues de Khéops ont permis à ceux qui en ont fait les relevés d’avancer avec rigueur l’angle d’inclinaison des quatres apothèmes de la pyramide. Cet angle tel que précisé dans l’ouvrage de J.P. Lauer est de 51°50’35”, le dessin n°11 montre un angle de 51°42’85”71, et les vérifications par le calcul suivant les valeurs de la calculatrice donnent un angle de 51°84’27”73 dixièmes. Les variations sensibles de toutes ces minutes trigonométriques importent vraiment lorsque l’on veut comparer les valeurs unitaires entre elles, ce pourquoi l’importance d’arrêter le nombre à son principe devient essentiel.

     L’ensemble des calculs sont ici déterminés suivant un angle de 51°84’27”73”’ afin de faciliter les vérifications éventuelles d’une première lecture, mais la nature des dessins impose cependant que des corrections trigonométriques permettent d’évaluer tous les angles suivant la valeur de 360/7 = 51°42’85”71”. La somme de temps nécessaire pour établir une valeur exacte de ces angles implique l’attention de recevabilité des démonstrations précédentes, ce pourquoi la patience oblige que maturation soit attendue afin de permettre toutes les comparaisons possibles.

     Si le temps nécessaire au calcul de tous les coéficients trigonométriques impose une longue recherche, l’essentiel est cependant démontré par l’étude de la coupe médiane de Khéops. Lorsque l’on compare les valeurs du dessin n°11 au précédent, l’étude permet de compléter l’hypothèse trigonométrique par le calcul des coordonnées au sommet de la pyramide lorsqu’il se situe sur le périmètre d’un cercle de 360 degrés. Le rayon du cercle mesure 57,272727, la base de la pyramide 11/14 fois le rayon soit 45 et le segment de longueur l’apothème mesure 72,836565. Cette valeur est 1,6185904 fois plus grande que 45 est 1,2714496 fois plus grande que la longueur du rayon.

     Reprenant le dessin de la page précédente, le calcul de l’angle de l’apothème avec la base de la pyramide permet de mettre en relief la géométrie fantastique de Khéops. Le dessin n°11 montrait un angle de 51°42’85”71 dixième dans le tracé d’un cercle de rayon la hauteur de la pyramide. Lorsque l’on dessine dans ce même cercle le triangle dans ses proportions pour situer le sommet sur le périmètre du cercle de rayon l’apothème, on obtient l’homothétie dans le rapport inférieur de 1,2717496.

AO = 7 = rayon du cercle.
OB = 5,5 = 44/8 = 45° linéaires.
AB = 8,9022472
CO = 7 = 44 / 2π
DO = 4,3247507
CD = 5,5042282
DF = 2,6752493 = AO x (1 – 1/ϕ)
AO =DF / (1 – 1/ϕ)
FC = √(2AO² x (1 – 1/ϕ))
L’arc FC = (OB / 3,5) x 4
L’angle COD = 51°42’85”71”‘
cos 51°42’85”71” = AO / 1,6185904 = DO
sin 51°42’85”71”’ = DO x 14/11 = DO x 4 / π
90 – 360 / 7 = 38,571428 = (45 / 3,5) x 3
38,571428 / π = 12,272727
12,272727 / 1,272727 = 9,642857 = π + 6,5

Périmètre de l’heptagone = 7 √(2AO² x (1 – 1/ϕ))
360 / (7 √(2AO² x (1 – 1/ϕ))) = 1,02709 = 44 / 7FC
(360 / 7) x 1,1438048 = 58,824247 = 57,272727 x 1,02709
((360 / 7) x π) / 50,072118 = 3,2279972 = π x 1,02709

1,6185904 / 1,02709 = 1,5758993
1,5758993 = (7j √(2AO² x (1 – 1/ϕ))) / 44

AO / DO = 1,6185904
AO / FC = 1,1438048
AB / CD = 1,617347
AB / FC = 1,4546333
OB / FC = 0,8987037
FC / OB = 1,1127137
AO / DF = 2,6165786 = 1,6175842²
45 / DF = 2,0558832
AB / DF = 3,32763267
FC / DO = 1,4150932 » √2 (1,4142136 x 1,000622 = 1,4150932)
FC / DF = 2,28760963 = 2AO/d

TX / AO = 1,6178215
FC = 2π/ 1,02709 = ((44 / 360) x 51,428571) / 1,02709
SX = PV = 14
QZ = 19,5
PZ = 21
TU / AO = 1 / 1,6175842²
UV / AO = 1 / 1,6185904

2,2876096 x 44/14 = 7,1896302 = 360 / 50,072118
2,28760963 / 2 = 1,1438048
1,1438048 x 44/14 = 3,5948151 = (d /OB) x π
3,5948151 x 44/154 = 1,02709

     La hauteur AO qui valait 7 unités, mesure en CD 5,5042282, la base OB qui mesurait,5,5 vaut en DO 4,3247507 et l’apothème AB de longueur 8,9022472 mesure par suite 7 en CO. L’homothétie correspond à un angle visuel dans l’espace de 19°07’86”16”’ dont le centre est situé à 20,23922 unités de longueur du centre O. La rotation effectuée de AO vers CO établit les proportions par ϕ de AO / DO = 1,6185904, AO / DF = 1/ (1 – (1/ϕ)) et AB / CD = 1,617347. Ces trois valeurs approchées de ϕ correspondent à:

1,6185904 = AB / OB = AO / DO
1/ (1 – (1/ϕ)) = 2,6165786 = 1,6175842² = 7/ (AO – DO)
1,617347 = AB / (AO – DO)

     Le segment FC est l’un des 7 côtés de l’heptagone inscrit dans le cercle de rayon 7 aux sommets, dont le cercle inscrit mesure 6,2957627 de rayon. La longueur de l’arc FC mesure 44/7 = 6,2857143 = 2π et le segment FC = 2π/ 1,02709. Cette valeur est celle qui définit la proportion relative du cercle à l’heptagone correspondant au périmètre d’un cercle de 360° divisé par le périmètre de l’heptagone égal à (7 √(2r² x (1 – 1/ϕ))). Lorsque le rayon du cercle mesure 57,272727, le périmètre de l’heptagone mesure 350,50482 et quand le rayon mesure 7, le périmètre est de 44 / 1,02709 = 42,839479. Le périmètre de l’heptagone divisé par 7 donne la longueur du segment FC = 6,1199255 = √(2AO² x (1 – 1/ϕ)) avec ϕ = 1,6185904.

     Lorsque l’on dessine √(2AO² x (1 – 1/ϕ)), le tracé donne la valeur de 2π/ 1,02709, de longueur √2 fois plus grande que DO à 1,0006221 près. Cette différence de 1,0006221 traduit également la fraction de 1,6185904 / 1,6175842. Les deux valeurs de AO² sont représentée par les deux carrés dont les côtés mesurent 7. La diagonale des deux carrés coupe leur milieu en E qui est le centre du cercle de diamètre 7. La longueur RV mesure AO x ((√5 + 1) / 2) = 7 x 1,618034. La valeur de 2π / 1,02709 est celle obtenue par la projection de √(OB² + (AO x sin (90 – 51°42’85”71”’))²) sur l’axe AO avec sin (90 – 51°42’85”71”) = DO. La hauteur de cette droite coupe la diagonale OG en H dont le segment OH est égal à FC.

     Dans le triangle EFO, l’arc de cercle de rayon DO coupe EO en I à l’intersection de EO avec le cercle de diamètre 7. L’arc FD détermine un point S dont la longueur jusqu’à l’extrêmité X de l’arc de rayon DO mesure 14 soit 2 AO. 
TU / AO = FD / AO = 1/ 1,6175842²
UV / AO = DO / AO = 1,6185904
TX / AO = 1,6178215

     Ces valeurs approchées du nombre d’or n’ont aucune récurrence, mais toutes trouvent leur proportionnalité dans le dessin de la pyramide. Si approximatif puisse paraître ce dessin, il permet cependant de démontrer la constante du rapport de π à ϕ = 1,6185904 dans un dessin ou toute la géométrie s’équilibre. La longueur OB est le périmètre divisé par 8 soit 44/8 pour un cercle de rayon 7 et 360/8 pour un cercle de rayon 57,272727. Cette proportion de OB dans un cercle de périmètre 360 mesure 45, soit le nombre de degrés de moitié un angle droit pour diviser le cercle en 7 et 8 secteurs égaux. La projection verticale de B sur le périmètre du cercle détermine un point de hauteur DO dont l’arc mesure (3 x OB / 3,5). Avec AO = 7, la longueur de l’arc mesure (3 x π/2). La droite AB est tangeante à l’arc de rayon DO. La projection horizontale de la hauteur B sur le cercle coupe la diagonale GO en H situé sur la droite CD. HO est de même longueur que FC qui est 1,02709 fois plus petit que 4OB/ 3,5. La longueur de SX est égale à (2FD + 2DO) = 2AO = 14, celle de PZ = 3AO = 21 et celle de QZ est (3AO – (3AO/14)) = 19,5. (CD / DO = 4/π = AO / OB), (CO / DO = ϕ = 1,6185904 = AB / OB) et ABO = 1,2717496 x COD. La proportion de 1,02709 à ϕ est égale à 1,5758993 = (7ϕ √(2AO² x (1 – 1/ϕ))) / 44, soit le périmètre de l’heptagone multiplié par ϕ/44. 

     De même si l’angle COD mesure 51°42’85”71”’, sin 51°42’85”71”’ = DO x 14/11 = DO x (4/π) et cos 51°42’85”71”’ = DO = AO / 1,6185904. Si l’on transpose ces mesures dans un cercle de périmètre 360 dont le rayon mesure 57,272727, le sinus de 51°42’85”71”’ est 45,034594, et le cosinus 35,384324. Le cosinus de (90 – 51,428571) est 45 et le sinus 35,384324. Ces deux inverses auraient dû présenter des résultats identiques, démontrés par la géométrie, sans l’arrondi des décimales sensiblement remarquable dans cette méthode de calcul, qui cependant, respecte toutes les proportions. CO = 7, DO = CO/ϕ et CD = 14DO/11.

     L’arc de cercle d’angle AOC mesure (OB / 3,5) x 3. Cette valeur est égale à 4,7142857 pour un cercle de rayon 7 et 38,571429 pour un cercle de rayon 57,272727. La longueur de l’arc de 38,571429 est également le nombre de degrés contenus dans l’angle AOC reporté 9,333333 fois sur tout le périmètre du cercle. Cet angle divisé par π est égal à 12,272727 cette valeur étant (((7 x 13)/14) x π) fois 4/π, ce qui là aussi, implique des régulations.

     Pour finir l’observation du dessin, restent à démontrer quelqu’autres propriétés remarquables dans le jeu des nombres et des proportions. Reprenant CF que l’on divise par FD, on obtient la valeur de 2,28760963 qui est égale à 2AO/CF. Cette valeur multipliée par 44/14 est égale à la proportion du segment de l’heptagone contenue dans le périmètre du cercle, soit 7,1896302 = 360 / 50,072118 pour un cercle de rayon 57,272727 et 44/6,1199255 pour un cercle de rayon 7. La moitié de 2,28760963 multipliée par 44/14 est égale à la moitié de 7,1896302 soit 3,5948151. Cette valeur est ((CF / OB) x π) qui, multipliée par 44/154 est égale à 1,02709. Cette valeur multipliée par π est égale à 3,2279972, soit (((360/7) x π)/ 50,072118) pour un cercle de rayon 57,272727 et (((44/7) x π)/ 6,1188255) pour un cercle de rayon 7.

     Avec le rayon d’un cercle de 360°, AO / CF est égal à 1,438048 soit 2,2876096 / 2. Lorsque l’on divise 360 par 7, que l’on multiplie 51,428571 par 1,438048, on obtient la valeur du rayon du cercle multipliée par 1,02709 = 58,824247. Cette valeur se reporte 6,1199253 fois sur le périmètre du cercle de rayon 57,272727 et 6,1199253 se reporte 7 fois sur chaque côté de l’heptagone du cercle de rayon 7. Le rayon du cercle de périmètre 360 divisé par 7 est égal à 8,18181818. Cette valeur divisée par 4/π est 45π/22 soit 6,4285711.

     Il serait évidemment d’intérêt de pouvoir mettre une limite supérieure à l’infini des relativité de ce dessin, les deux valeurs de π et ϕ étant exprimées dans leur géométrie mathématique par laquelle tous les recoupements son possibles. Ces nombres deviennent vite un jeu, un enthousiasme et pour finir une fascination qui n’a de cesse de surprendre et porter loin la volonté de poursuivre, mais comme un bel ouvrage auquel il se faut consacrer du temps, de la concentration et l’organisation essentielle à la mémorisation de tous les nombres. Des questions restent en tourment, des points à découvrir, des hypothèses à démontrer et des synthèses à poursuivre. Mais le temps viendra où Khéops sera un mystère, celui qui laisse à voir, à connaître, à comprendre, sans ne jamais savoir comment, en des temps si lointains, cette pyramide à pu éveiller le jour.

     Le temps de conclure fait appréhension et le dernier mot ne veut pas de fin, comme si déjà il serait vain de vouloir arrêter le temps des rêves. Portés en ces sphères de la fantaisie de chercher, les rêves font mathématiques de l’enchantement à dénombrer le nombre qui saisi par l’esprit la géométrie des formes pour exercer la vision dans l’espace du dessin. L’espace se dessine par lignes abstraites dans la plus pure harmonie qui le compose dans le temps.

     Le temps a fait ses gammes dans les plus beaux traités d’histoire et la vie serait triste si nous ne pouvions en jouer un peu, par goût peut-être du murmure dans le vent des formules qui ont créé tous les génies du passé. Platon, Euclide, Archimède, Pythagore, ces noms appris dès l’enfance à l’école ont grandi par les rêves tous les maîtres qui enseignaient ces savoirs de jadis de nos maîtres ancestraux, qui d’ailleurs nous venaient pour traduire de l’espace toute l’essence vitale de la géométrie. Savoir, compter, mesurer, connaître, tout ce qui dans la vie apaise l’esprit, transforme le tourment en véritables questions, et résoud par le temps les ineffables locutions de pensées par trop vives embrumées de burlesque.

     Comme une petite lumière, ces noms continuent de faire oeuvre vive quand ils portent courage d’exprimer la pensée, celle passive du ressentiment que l’obséssion fini par vouloir démontrer. Les nombres tracasses, ils entortillent, ils mettent par force face à la question de savoir en soi ce qu’est la forme pensée de toutes les années consacrées au pupitre pour retenir de leur essentiel fondement ces noms qui illuminent l’histoire. Les théorèmes sont des points capitaux qui font de mémoire l’usage des formes ce par quoi il faut essayer de faire bel usage de cet esprit, loin de l’antique mais par bienfait d’une vie plus sobre en certitudes pour à nouveau pouvoir essayer de grandir les tableaux d’école.

     Le Nombre d’Or fait grandir cette question de l’enseignement qui n’existe plus, de savoir par géométrie conçus qui n’ont plus oeuvres d’architecture, plus de maintien pour faire l’espace dans le nombre des proportions. ϕ est devenu un symbole et π reste un moyen de compter les niveaux de l’échelle qui conduisent à l’exhaussement. Du connaître pour savoir ne reste plus à cette mesure que le sentiment de compter par trop de fois le même fondement. Bâti dans le temps pour arrêter un principe, le nombre n’est plus qu’un moyen ingénieux de faire des quotations par mesures averties des sentences linéaires qui accompagnent le nombre. Décimales infinies d’un cercle qui ne l’est pas les pointillés du moderne laissent un goût d’amertume au fruit de cette nature par génie dessiné pour mûrir dans l’esprit par sa simple évidence.

3,14159265358979323846264338327950288419716939937510…

     Cinquante décimales qui pouraient faire la ronde du périmètre terrestre passant à l’équateur, pendant qu’en ce temps il suffit de compter 3,142857 puis de moitié s’amuser à narguer 1,571428, et poursuivre par la fantaisie d’ajouter 6,285714 puis faire repos d’une ultime moquerie par 0,142857. Le théâtre en ce nombre et si grand de clarté que toutes perspectives de déroulent par les yeux.

0,14 28 57 14
0,28 57 14 28
0,4 28 57 14 2
0,57 14 28 57
0,7 14 28 57 1
0,8 57 14 28 5
1
1,14 28 57 14
1,28 57 14 28
1,4 28 57 14 2
1,57 14 28 57
1,7 14 28 57 1
1,8 57 14 28 5
2
2,14 28 57 14
2,28 57 14 28
2,4 28 57 14 2
2,57 14 28 57
1,7 14 28 57 2
1,8 57 14 28 5
3 
3,14 28 57 14

Et cætera, et cætera….

     Mais la conclusion la plus drôlatique est sans doute dans l’humour de pouvoir affirmer que cet angle qui reçut par toutes sortes de nombres, l’appellation nominale de leurs génies, reçoit en cet an la dernière claironnade pour sonner le toxin de leurs contredits. 51°42′ 85” 71”’ est 360 fois le 22ème de π, petit symbole qui fait mine des l’âges qu’unités en degrés il démontre grandis.

     Les nombres qui ont construit ici la montagne sont de dix unités de 0,14285714. Les décimales qui démontrent le nombre sont de 1,42 85 71 qu’il suffit de produire 36 fois pour obtenir la valeur de l’angle. Dans cette logique de l’harmonie des nombres, il devient possible d’exprimer ϕ par l’unité qui divise le cercle en 360 degrés de angle inscrit de la base au sommet.

     Si “p” est le périmètre d’un cercle de rayon 7, si u = 0,14285714, et
ϕ = {(√(r² + (p/8)²)) / (44/8)}, alors ϕ = 8{(√(49u² + (308u/8)²)) / (308u)} =
8 ((√(317 / 4)) / 44) = 1,6185904. Ces formulations ont le dessin d’un nombre d’or pyramidal, surprenant, et magnifiquement inscrit dans l’harmonie d’un nombre hors du commun, qui pourtant fait l’ingéniosité du cercle dans sa simplicité la plus logique.

     Et l’irronie n’arrête pas le rire quand on poursuit le dessin. L’angle de 51°42’85”71”’ étant divisible par une unité multiple de 36, dix fois comptée par l’unité de π, il est logique de pouvoir penser qu’il en va ainsi des autres angles. Lorsque l’on dessine l’apothème dans le cercle de rayon sa hauteur, le cercle est 1,2717496 fois plus grand que celui de rayon 7 et 1,6185904 fois la largeur de la demi-base longue de 5,5 unités. La valeur de ϕ, comprise 5,5 fois dans le rayon du cercle est 8 fois la 44ème division de AO correspondant à huit unités d’un cercle de périmètre AO dont le rayon mesure 1,4162665 = OG, l’unité 0,2023237 et les huit unités du 44ème de périmètre 1,6185904.

Avec AO = 8,9022469
OB = 5,5 = AO / 1,6185904
CO = 8,9022469
DO = 4,6790239 = CO / 1,9025863
CD = 7,5734232 = DO x 1,6185904
DF = 4,223223 = AO – DO
FC = 8,6713522
L’arc FC mesure 9,0571433

Avec AO = 57,272727
OB = 45
CO = 57,272727
DO = 30,102564
CD = 48,723721
DF = 27,170163
FC = 55,787263
L’arc FC mesure 58,269254 correspondant au nombre de degrés portés sur le périmètre du cercle.

BI = 7
HI = 5,5
AO / 14 = 1,2717496 unité proportionnelle à l’unité 1.
AO / 11 = 1,6185904 unité proportionnelle à l’unité 4/π
OB / AO = 0,78571428 = 0,5 + (π/11)
OB / DO = 1,1754588 proportion de AOB à celle de COD.
OG = 1,4162665. Le périmètre du cercle mesure AO.

     Dans le cercle de rayon 7, l’unité proportionnelle à l’angle de 51°42’85”7”’ est multiple de π/22 comprise (3,5 x 11) fois dans la longueur de 5,5 et 360 fois dans la mesure de l’angle. Si l’on divise la longueur de AO = 8,9022469 par le nombre de degrés compris dans le rayon d’un cercle de périmètre 360°, l’unité du cercle mesure 8,9022469 / 57,272727 = 0,155436. Cette valeur multipliée par ϕ = 1,6185904, donne la valeur de l’unité ϕ fois plus grande que celle qui divise le cercle de rayon 7 par l’unité comprise dans la largeur de 5,5. L’unité de 0,155436 multipliée par ϕ mesure 0,2515873 comprise 36 fois dans la longueur de l’arc de 9,0571433.

     Pour trouver la mesure de l’angle COD, il suffit ensuite de diviser le rayon du cercle de 360° par celui du cercle de rayon AO pour trouver la proportion qui, multipliée par 9,0571433 permet de trouver la valeur de l’angle. Le rayon de 57,272727 / 8,9022469 = 6,4335137 qui multiplié par 9,0571433 permet de trouver un angle de 58°26’92”54”’, 36 fois plus grand que la valeur de ϕ et 288 fois celle de AO / 44. Le cosinus de cet angle mesure 0,5256003 et le sinus 0,8507316, ϕ fois plus grand que le cosinus. L’angle AOC mesure (90 – 58°6’92”54”’) = 31°73’07”46”’, le cosinus mesure 0,8507316, ϕ fois supérieur au sinus de 0,5256003.

     Lorsque l’on compare toutes ces valeurs à celles obtenues par le dessin précédent, il est à remarquer que OE sur ce dessin est égal à DO sur le dessin précédent, le segment OB de longueur 5,5 coupe le cercle de rayon AO en un point I de hauteur 7 formant un angle IOB de 51°42’85”71”’ dont l’arc mesure (4 x (π/2) x 1,2717495).

     En poursuivant le dessin par la diagonale de la pyramide, le rayon du cercle mesure 10,464225 en AO, la base du triangle mesure (5,5 x √2) en OB et la hauteur du triangle mesure 7. Dans les proportions unitaires de la pyramide, ce triangle correspond à une hauteur de 4/π pour que la base mesure √2. Ces valeurs reconstruites par le cercle de rayon 57,272727 correspondent à 45 unités de 1,272727 pour le rayon et ((100/√2) x 1,272727) pour le quart de périmètre de longueur 90 degrés. Le rayon de 45 unités divisé par 7, multiplié par (5,5 x √2) unités correspond à la longueur de 50 unités de la base proportionnellement au quart du périmètre du cercle.

     Dans le cercle de rayon 4/π, le périmètre mesure 8, l’arc de l’angle à 45° mesure 1 et la longueur OB = (1 x √2). Ce cercle, 45 fois plus petit que celui de périmètre 360° correspond au dessin unitaire du triangle dont la hauteur mesure 7 et la base 5,5 de moitié les proportions de la pyramide de 14/11. Lorsque l’on divise la hauteur du triangle de 1,272727 par 11, on obtient l’unité 360 fois plus petite que la valeur de l’angle BOC. L’angle mesure 41°65’28”92”’ correspondant au périmètre de 360° divisé par 44, multiplié par 4 puis 1,272727. Dans le cercle de rayon 7, la valeur de l’angle est celle de l’arc coupé par la droite OC dont la longueur est de 5,0909090 unités. Cette valeur divisée par 44 et multipliée par 360 correspond à l’angle de 41°65’28”92”’. Le cosinus mesure 0,7433111, le sinus 0,6689458 correspondant à la hauteur de 7 unités, la largeur de (5,5 x √2) et l’hypothénuse (√438)/2. Dans le cercle de rayon 4/π, le sinus de 45° multiplié par 1,272727 mesure 0,8999541. Cette valeur est égale à 1,272727 x
tan 41°65’28”92”’ dans la proportion du rayon du cercle de longueur (1 x 4/π).

L’unité qui divise l’angle de 51°42’85”71”’ est de p/22 = 0,14285714 multipliée par 10 puis 36. L’unité qui divise l’angle de 58°26’92”54”’ est de j/10 = 0,16185904 multipliée par 10 puis 36. L’unité qui divise l’angle de 41°65’28”92”’ est de (4/p)/11 = 0,1157024 multipliée par 10 puis 36. Ces unités sont celles qui divisent également la hauteur de la pyramide et l’apothème correspondant à la hauteur de chacun des triangles dans la proportion de la base. Quand la base est divisée en 11 unités de 1, la hauteur de l’unité proportionnelles à l’unité de la base du triangle mesure p/22. Quand la base est divisée en 11 unités de Ö2, la hauteur de l’unité proportionnelle à l’unité de la base du triangle mesure 4/p. Quand la hauteur du triangle est celle de l’apothème l’unité proportionnelle à celle de la base du triangle mesure j.

     Les unités qui ont servi au calcul des angles sont celles qui divisent chaque segment de la pyramide suivant le principe démontré par le dessin n°11 et avec les certitudes appliquées de cette géométrie. Mais il semble improbable de pouvoir définir une règle qui voudrait que par l’unité donnée d’un triangle, la multiplication par 360 arrivent à la mesure de l’arc. Les résultats obtenus pour le calcul des deux angles de 58°26’92”54”’ et 41°65’28”92”’ furent d’abord intuitifs, puis seulement dessinés mais difficilement démontrables dans le tracé du dernier dessin. La diagonale de la pyramide est l’élément le plus sensible qui impose une étude indépendante des autres faces pour mettre par l’évidence le point sur les proportions qui régulent les trois unités de sa triangulation. La division de 4/π pour obtenir l’unité de cet angle est une incohérence pourtant remarquable par le fait que tout de logique semble pouvoir s’accomoder de calcul pour le moins à démontrer.

     La superposition des trois dessins précédents permet de mettre en évidence les propriétés remarquables de la pyramide dans le dimensionnement croissant des trois sections. Cette progression suit une logique de l’espace qui de l’unité 1, projette par homothéties et rotations toutes les valeurs unitaires des autres faces. Ces valeurs pour être exprimées, impose cependant l’usage de la calculatrice pour vérifier par juste rigueur les valeurs trigonométriques de Khéops.

Angles obtenus par la calculatrice	Angles résultant de leurs divisions unitaires
α = 51°84’27”73”’ β = 38°15’72”27”’ χ = 58°29’13”34”’ δ = 31°70’86”66”’ ε = 41°98’57”59”’ φ = 48°01’42”41”’ γ = 45°	α = 51°42’85”71”’ β = 38°57’14”29”’ χ = 58°26’92”54”’ δ = 31°73’07”46”’ ε = 41°65’28”92”’ φ = 48°34’71”08”” γ = 45°

     Ces angles apparemment différents sont malgrés tout les mêmes suivant une valeur attribuée à π qui ne varie que sur le périmètre du cercle. Une vérification immédiate permet d’en traduire le fait lorsque l’on multiplie tan 41°98’57”59”’ à 1,272727. Le résultat est de 0,8999541 fois la mesure de 4/π du rayon du cercle porté sur le troisième dessin. Ces variations de minutes sont le résultat d’une géométrie qui attribue à π la fonction pratique de pouvoir mesurer le cercle par la longueur du rayon dont l’unité se compte par des nombres entiers.

     Progressivement mise en élévation dans l’espace, l’unité se dévoile par son expression d’une mesure symboliquement définie pour établir la grandeur du nombre 1. Mise en plan sur quatre face, l’unité se transforme en quantités de mesures inscrites par le trait de segments de valeur 1 dont la proportion variable ne change que par l’expression. Le nombre d’or est ici l’unité de 1 porté dans l’espace par divisions de l’horizon en chaque point d’élévation de l’oeil. De là des proportions, des additions, des multiplications et toutes les divisions qui établissent les rapports unitaires.

     Le doute sur la nature des régulations géométriques est bien évidemment permis, mais plus sans doute sur la valeur d’interprétations hazardeuses qui viendraient à vouloir prouver que les architectes de Khéops aient délibéremment voulu attribuer à leur pyramide toutes les valeurs mathématiques que la géométrie démontre. La géométrie en fait, n’a que l’essentielle facilité du dessin pour parvenir à dérouler le fil d’une idée, cousue d’or par cette volonté première de mettre en oeuvre un concept, celui de l’espace édificateur de l’harmonie.

     L’inclinaison des faces de Khéops fut conçu, ce qui en résulte est moins certainement attribuable à la pure volonté de mettre en chaque angle ce que la pyramide entière exprime dans les proportions de la base et l’élévation du sommet. Il n’est pas moins vrai que cette pyramide est un véritable tableau révélateur de toutes les connaissances antiques, et sans doute au delà des faits attribuables aux révélations de papyrus comme de celui de Rhind. Si les réfutations se veulent affirmer par l’absurde l’irrecevabilité d’un concept géométrique de Khéops, aucune raison ne le démontre plus raisonnablement que la conviction inverse de voir là une oeuvre, divinement construite et pour le bienfait de l’humanité entière qui empreinta son essentiel fondement dans la régulation d’une architecture pensée, construite, élevée par le nombre.

     “Avant d’achever cette description des mathématiques et de l’astronomie égyptiennes, il nous faut dire un mot de ce qu’en bien des ouvrages on appelle encore la “science secrète des Pharaons”. Il n’est pas inutile de rappeler que nous ne savons rien d’une telle science, et qu’il est des plus douteux qu’elle ait jamais existé. Toutes les spéculations qui ont été faites sur les “chiffres” de la Grande Pyramide, entre autres, sont de purs enfantillages; tel aurait été le cas même si les auteurs avaient utilisé des mesures et des nombres exacts, ce qui est loin d’être vrai. Pourquoi d’ailleurs la “Grande Pyramide”, seule, nous aurait-elle transmis, d’une façon obscure et, pour tout dire, impénétrable, une science si avancée qu’elle dépasse la science grecque et s’apparente à la science moderne? Il y a dans la vallée du Nil, depuis le delta jusqu’au Soudan, plus de 150 pyramides, et seule celle de Chéops nous donnerait la vraie valeur de π, la dimension du rayon de la Terre et la mesure exacte d’un arc du méridien terrestre ? On voit l’absurdité de cette position, fondée, rappelons-le, sur des mesures inexactes.”

La Science Antique et Médiévale
Des origines à 1450.
René Taton
Quadrige – Puf

     La seule vérité qui puisse ressortir de tel propos s’apparente à l’objet du chapitre parcourus. Trop de vérité par trop justement démontrées viennent à éteindre l’essentielle attention qu’il faut consacrer à la lecture de Khéops. La pyramide est avant tout un concept exprimant par volonté l’expression de quelques nombres et ceux-ci seulement sont de vérité à dévoiler tout ce que les sciences passées ont pu faire naître de connaissances à la fois de la géométrie et de la Terre. La trigonométrie fut inventée en Inde et l’astronomie n’eut qu’une apogée tardive. Mais ce qui reste d’essentiel à tout cela est sans doute la globalité d’événements considérables qui tous ont bâti par logique ce monument.

     Comme l’étoile dans le ciel, il n’y a jamais de solitude dans le fait de son existance, car observée sous les astres, elle appartient à l’univers entier. La pyramide est de ces lumières qui attisent les pensées les plus vives à ceux qui en font raison de voir là deux monuments en un lieu d’identique nature. Le premier est Khéops, le second moins apparent est sa parfaite réalisation dans la volonté de deux nombres qui énumèrent toutes les sciences telles que voulues des modernes, héritiers d’un passé qui a conquis ses origines aussi loin que toutes celles transmises par l’Egypte.

     Le secret des Pharaons n’est pas discutable au vocable de ceux qui n’y voient rien de cette splendide beauté de Khéops, de loin plus aboutie que la pyramide de Meïdoun et par vue mieux pensée que celles d’après, car seule d’Egypte à parfaire le nombre comme aucun autre monde n’a pu le penser. La Grèce, la Chine et sans doute d’autres sphères eurent conscience de la valeur d’importance de mesurer le cercle, mais Khéops en fut sans doute la seule construction la plus authentique, et par preuve de ce qui est dans le dessin transmissible de ce savoir vieux de 4600 ans.

     L’enfantillage d’une question, puis celui de démonstrations, et sans doute par suite d’erreurs, porte malgrè tous les discrédits pensables d’échos, cette satisfaction d’avoir cousu de recherches personnelles la part immense des rêves que la pyramide inspire en Khéops. Je ne l’ai vue que sous cet angle de la géométrie imagée sans ne jamais parcourir d’un seul pas le seuil du sommet, trop haut sans doute pour en percevoir l’idée intérieure que l’imaginaire s’est construit. Mais ce que j’en crois est merveilleux, ce que j’en pense est consciencieux et ce que j’imagine fait le secret qui est au Pharaon l’unique flagrance.

     Du temps de cet au-delà qui est à l’humanité un berceau éternel, il a fallut des noms, et des plus grands, pour que la beauté parvienne à faire sens prenant d’un imaginaire incréé dans la forme de Khéops. D’apparence subtile, de technologie prouvée, de style imprenable, rien malgré tout ne prédispose l’idée à voir là une magie, un événement merveilleux qui en son antre a conçu le monde autrement que par le fait d’une géométrie discutable autant que l’objet de son architecture. La pyramide n’a de beau que son ampleur dans les sables pour faire masse contre vent, fastes contre le temps comme l’astre sous le soleil.

     Il n’y avait en deçà que l’absence d’origines humaines pour établir cette importance là de trouver en Egypte les fondations de l’Homme, celui idéalement conçu dans le propos des plus grands qui voulaient de par le monde inventer les sciences de l’humanité. La philosophie regardait les peuples, l’astronomie les étoiles. Les mathématiques ont regardé l’Egypte comme unique point d’observation désignant toutes les connaissances du nombre. Enuméré, il entrait dans l’espace pour construire, édifier le déploiement d’une science pratique de la matière que la géométrie façonnait par les lignes projetées de sa transformation.

     Dessin d’un imaginaire instruit, ordonnancé, concepteur de l’organisation interne des éléments, la géométrie est l’idée plane d’un espace imperceptible au regard pour traduire dans son fondement le mouvement de la forme réalisée. Le cheminement de l’idée en fait le tracé, progressivement construit par l’attention première de démontrer, énoncer les formulations de l’espace pour le rendre descriptible dans la logique perspective de l’oeil qui construit la pensée. Langage des nombres par le trait, mathématique arrêtée au fini du dessin dont la ligne fait l’objet d’équations construites, la géométrie est surtout un moyen de comprendre la réalité du nombre dans sa proportion relative à l’espace.

     Ecrit de pierres, dessiné de pensées, traduit par l’idée d’énoncer un concept, le nombre est l’indéniable monument qui couronne Khéops de ce mystère secret de la géométrie. Dénoncé par l’invraisemblance, détrôné par l’incohérence de vastes rêveries, le nombre en Khéops est devenu l’anodin coutumier d’une époque aguerrie de sciences. Mais il faut continuer, ne pas arrêter le temps aux anciennes certitudes qui voudraient que tout soit dit, accompli dans le précepte de l’agrément des contemporanéïtés. Il faut, comme les montagnes, se dire que Khéops est bien jeune et promise à d’autres avenir que l’oubli, d’autres splendeurs que jadis, d’autres grandeurs que par π. Le nombre d’or en est l’écho, voué à faire mont de cette merveille.

     Lorsque l’on dessine la progression de l’unité 1 dans l’espace, les translations et rotations en chacun des angles permettent d’obtenir les variations proportionnelles des divisions de la pyramide dans le rapport de 14 à 11, puis 7 jusqu’à réduction au sommet. La hauteur de la coupe médiane de la pyramide divisée en 14 unités détermine la valeur 1 de la progression. Cette valeur multipliée par 1/ cos 51°84’27”73 mesure 1,6185904 par projection sur la hauteur de l’apothème. L’apothème mesure √317, la valeur de ϕ = 1,6185904 est contenue 11 fois dans la hauteur de l’apothème correspondant à ϕ = √317 / 11 = √(14² + 11²) / 11. La valeur de ϕ à une inclinaison de 51°84’27”73”’ avec la base de la pyramide, la hauteur verticale est de 4/π dont la mesure divise la hauteur de la pyramide en 11 unités. La projection au sol est de 1 soit 11 / 11.

 

     Poursuivant la progression dans l’espace, la mesure de ϕ est multipliée à
1/ sin 58°29’13”34”’ jusqu’à la onzième division de l’angle de la pyramide. L’arête d’angle mesure √438, cette longueur divisée par 11 vaut 1,9025863, soit 1 x 1/ cos 58°29’13”34”’. L’unité de 1,9025863 a une inclinaison de 41°98’57”59”’ avec la base de la pyramide, la hauteur verticale mesure 4/π et la projection au sol √2. La droite passant par ϕ et 1,9025863 est parallèle au plan du sol. Dans le plan de la face de l’apothème, l’unité de l’hypothénuse est de √438 / 11, la hauteur verticale mesure ϕ, l’unité au sol mesure 1 et le segment de longueur √438 / 11 a une inclinaison de 58°29’13”34”’ avec le plan au sol de la pyramide.

     Sur la deuxième face de la pyramide, la hauteur de l’unité sur l’arête d’angle multipliée par π/2 permet d’arriver sur l’axe de l’apothème à la hauteur de √317 divisée par 7. Dans le plan de l’apothème, la hauteur verticale de √438 / 11 mesure ϕ. Cette valeur étant 11 fois plus petite que la hauteur de la pyramide, le produit jusqu’à la division de la hauteur par 7 est de π/2 mesurant sur l’axe de l’apothème 2,5434991. Cette valeur est également celle de l’unité verticale de hauteur 2 multipliée par
1/sin 51°84’27”73”’. L’unité de √317 / 7 a une inclinaison de 51°84’27”73”’ degrés avec la base de la pyramide, dont l’unité au sol mesure π/2.

     La droite passant par √438 / 11 et √317 / 7 coupe l’autre arête d’angle de la pyramide à la hauteur de 3,9969276. L’inclinaison de cette mesure fait un angle de 41°98’57”59”’ degrés avec le plan du sol. La projection verticale mesure 2,6737716 de hauteur dans la proportion de 1,4948892 avec l’unité de longueur 3,9969276. Cette proportion est également celle de 1 x 1/ sin 41°98’57”59”’ = 1,4948892 = √438 / 14 = (√438 / 11) / (4/π). Lorsque l’on divise 2,6737716 par 1/sin 41°98’57”59”’, la hauteur sur le plan vertical de l’axe de la pyramide est de 1,7886085 inférieure de 0,2113815 à l’unité 2. Cette réduction est due à l’inclinaison de la droite dessinée sur la face de l’apothème dans la proportion de π/2 entre √438 / 11 et √317 / 7.

     Le tracé de 3,9969276 sur l’arête d’angle est reproduit sur la hauteur de l’apothème de la troisième face de la pyramide. La projection verticale mesure π en hauteur et 2,4693878 soit π/2 x (11/7) = (π/2)². La valeur de π/2 correspond à l’unité au sol de la projection verticale de √438 / 7 dont la hauteur dans la plan de l’apothème mesure 2,5434991 = √317 / 7. Le produit de √317 / 7 par 1 / sin 58°29’13”34” permet d’obtenir la longueur de √438 / 7 = 2,9897785 dont l’inclinaison dans le plan de l’apothème est de 58°29’13”34”’ et celle dans le plan au sol de la pyramide 41°98’57”59”’.

√317 / 14 = 1,2717496 = 1 x 1 / sin 51°84’27”73
√317 / 11 = 1,6185904 = ϕ = 1 / cos 51°84’27”73”’
√317 / 7 = 2,5434991 = 2 x 1 / sin 51°84’27”73”’
√438 / 14 = 1,4948893 = 1,2717496 / sin 58°29’13”34”’
√438 / 11 = 1.9025863 = (4/π) x 1 / sin 41°98’57”59”’
√438 / 7 = 2,9897785 = 2 x 1 / sin 41°98’57”59”’

AB = 1,272727
AC = √317 / 11 = 1,6185904
AD = √438 / 11 = 1,9025863
AE = AC = 1,6185904
FG = AB x 1,57142857 = (4/π) x (π/2) = 14/7 = 2
FH = AE x 1,57142857 = √317 / 7 = 2,5434991
FI = AD x 1,57142857 = √438 / 7 = 2,9897785
IH = ED x 1,5714286 = π/2 = 11/7
FJ = FH = 2,5434991
KJ = FJ x 1,57142857 = 3,9969276
KL = FG x 1,57142857 = 3,1428572
JL = IH x 1,57142857 = (π/2)² = 2,4693878
JM = FI x 1,57142857 = 4,6982234
MN = 1,4960383 x (π/2)² = 1 x 1/ sin 41°98’57”59”’ x (1,57142857)²
MO = 1,4960383 x (π/2)² x 1/ sin 41°98’57”59”’ = (1,4960383)² x (π/2)²
MP = MJ = FI x 1,57142857 = 4,6982234
JN = 1,1754588 x (π/2)² = (AD / AE) x (1,57142857)²
Les valeurs de MJ, JN, MN, MO et MP sont à démontrer, mais avec le temps nécessaire à l’étendue de cette étude.

     Toutes ces valeurs expriment une progression dans l’espace dont la valeur de π/2 permet de gravir chaque face suivant un rapport constant des mesures à l’unité. Mais s’il est aisé d’en établir le calcul sur les valeurs entières des unités de base, l’élévation diversifie le calcul suivant la réduction de chaque face dans la hauteur de la pyramide. Si l’on calcul la hauteur de la droite qui conduit sur la quatrième face de la pyramide, la valeur portée sur l’arête d’angle mesure 5,5225681, la hauteur par projection verticale est de 3,6942989, l’unité sur le plan au sol mesure 2,9026636 et la verticale dans le plan de l’apothème mesure 4,6982234.

     Bien qu’incertaines, ces valeurs sont à démontrer avant d’avancer de quelconques conclusions, pour comprendre la véritable progression qui conduit du périmètre de la pyramide jusqu’au sommet dans un rapport de réduction de valeur π/2. Cette valeur est celle qui détermine le périmètre d’un quart de cercle dont le rayon mesure l’unité de la face précédente, et chaque face de la pyramide représente le quart de périmètre d’un cercle de rayon la demi-hauteur de la base au sommet. La progression de π/2 sur chacune des faces détermine le dessin d’une spirale dont la progression s’accélère vers le centre, alors que l’objet du calcul vise à trouver la progression dans le rapport de π/2 qui permette d’atteindre le sommet suivant une progression ralentie, proportionnelle à la réduction en coupe de l’élévation des quatre faces de la pyramide.

     Ce dessin en démontre le principe suivant une progression de 1ϕ sur chaque arête d’angle de la pyramide jusqu’au pyramidion du sommet. Celui-ci mesure chacune des unités de 1 en hauteur, ϕ pour l’apothème, π pour la largeur de la base et 1,9025863 pour la longueur de chaque arêtes.  La ligne de progression 1ϕ débute à la hauteur de 4,6982234 en projection verticale de la mesure portée sur la quatrième arête, l’extrêmité suivante passe à 4ϕ puis 5ϕ, jusqu’à 11 qui détermine la pointe du sommet de la pyramide. Les valeurs intermédiaires portées sur chaque hauteur d’apothème sont les suivantes:

A	B	C
Hauteur sur l’apothème.	Hauteur de la projection verticale.	Longueur de la projection portée sur le plan du sol.
5,5079441	4,3309971	3,4029265
7,2836568	5,727272	4,5
8,9022472	7	5,5
10,520838	8,2727268	6,5
12,139428	9,545454	7,5
13,758018	10,818181	8,5
15,376609	12,090909	9,5
16,995199	13,363636	10,5

A / B = 1,2717497

A / C = 1,6185904

B / C = 1,272727

     Cette progression multiple de ϕ = 1,6185904 permet uniquement de rendre par l’image la valeur d’une hypothèse qui reste a devoir être démontrée pour établir la progression linéaire d’une pente qui puisse conduire de la base jusqu’au sommet. Les quatre face de la pyramide sont d’égale longueur, leur somme est le périmètre d’un cercle de rayon la demi-hauteur, et la progression se dessine par une spirale déroulée autour d’un cône de hauteur 14 dont la base du cercle mesure 7 de rayon. Cette spirale dessinée dans les proportions de la pyramide, correspond au dessin mathématique d’une sphère qui sans doute, inspirât les même interrogations que toutes celles posées par Archimède dans ses travaux.

     L’étude détaillée de l’espace de Khéops necessite que le tracé de la ligne de progression fasse l’objet de dessins comparés pour en déterminer toutes les valeurs. Seul le temps peut oeuvrer en ce sens pour parfaire le calcul des unités aux angles suivant la géométrie de dessins qui puissent être démontrés. L’évolution doit pour ce étayer l’hypothèse de toutes les connaissances inspirées par les régulations qui définissent les trois faces triangulées de la pyramide. L’étude portée sur les proportions de Khéops voit ce qui suit compléter sommairement ce que l’étude des angles a pu mettre au jour de connaissances jusqu’alors inaperçues.

     La progression de l’ensemble des mesures a pu montrer dans les dessins précédents que les valeurs régulées de chaques faces sont multiples des proportions de π. L’écriture courante de π énumère les décimales du quotient des deux entiers qui divisent chaque face par 11 puis 7, et ce dans la progression qui va de 1 à π. Il résulte de ces deux nombres un déplacement de l’unité dans l’espace qui permet de définir une valeur perspecive de π. L’écriture a pour mesure l’unique angle de l’apothème dont l’inclinaison de 51°84’27”73”’ permet de dessiner l’idiome trigonométrique de π.

π = 1/ sin 51°84’27”73”’ x 4 x cos 51°84’27”73 = 3,14285714.

     Cette valeur comparée au dessin n°11, correspond à quatre hauteurs d’apothème, divisées par 14 et multipliées par cos 51°84’27”73”’. Dans le tracé du dessin n°35, la valeur de ϕ = 1/ cos 51°84’27”73”’ est multipliée par 1/ sin 58°29’13”34”’ puis π/2, divisée par 1 / sin 41°98’57”59”’ et multiplié par π/2. L’écriture de {sin 41°98’57”59”’ / (cos 51°84’27”73”’ x sin 58°29’13”34”’)} étant égale à 1,272727, cette valeur multipliée à π² / 4 mesure π. La proportion de ϕ à π est de {(sin 41°98’57”59”’ / sin 58°29’13”34”’) x π² / 4 } dont la longueur est égale à 1,94172490 = 22π/ 7(√(16 + π²)). Avec
1/ sin 51°84’27”73”’ multiplié par 1/ sin 58°29’13”34”’ puis π/2, divisé par
1/ sin 41°98’57”59”’, le produit est multiplié par deux pour arriver à π. L’écriture de {sin 41°98’57”59”’ / (sin 51°84’27”73”’ x sin 58°29’13”34”’)} étant égale à 1, la valeur de 2π/2 mesure π. 

     La valeur de 1/sin 51°84’27”73” mesure 1.2717496 contenue 14 fois dans la hauteur de l’apothème, tan 51°84’27”73”’ mesure 4/π contenue 11 fois dans la hauteur de la pyramide, la valeur de 1/ sin 58°29’13”34” mesure 1,1754588 contenue 17,804494 fois dans l’arête d’angle de la pyramide. L’arête d’angle mesure √438 et l’apothème √317,
1/ sin 58°291334 = √438 / √317. La valeur de 1/ sin 41°98’57”59”’ mesure 1,4948892 contenue 14 fois dans l’arête d’angle de la pyramide. Le nombre d’or, dans la pyramide mesure {(4/π) x 1/ sin 51°84’27”73”’}.

     Ces nombres, proportionnés dans la pyramide, permettent d’établir la relativité des irrationnels tels que formulés suivant les proportions de Khéops dont la hauteur de 14 et la demi-largeur de 11 représentent les entités de mesures variables sur chaque plan d’observation. Vue en coupe axiale, la pyramide détermine l’unité première indivisible par laquelle sont ensuite produites les unités les plus grandes sur les quatres faces de l’apothème et la diagonale qui passe au sommet. Cette division des faces par proportionnalités permet de calculer chaque variable suivant les mesures entières de la géométrie formulées en dimensions du nombre 1.

     Ce nombre dans la hauteur de Khéops mesure une coudée de 0,47619048 mètres, le nombre ϕ mesure 0,77075734 mètres, l’arête d’angle divisée par 11 mesure une unité de 0,905993494 mètres l’apothème divisé en 7 mesure 1,21119007 mètres et la racine de 2 d’une coudée mesure 0,673435035. Ces valeurs irrationnelles n’ont d’autre expression que leurs proportions dans les mesures entières de cette architecture, qui pour être définie, doit terminer le dessin par où suggérées ces valeurs unitaires s’inscrivent dans un plan.

     Seule face visible de la pyramide, l’apothème semble à l’oeil différent du dessin qui déploie en hauteur le gigantisme perspectif d’un horizon infini de la masse. Monumental au regard humain il l’est aussi dans ses dimensions hautes de 186,52327 mètres sur le plan incliné de Khéops. Démesure incalculable qui échappe à la vision d’un homme mis au pied d’une géométrie 110 fois plus commensurable que la hauteur d’un oeil mis au fait de percevoir d’en bas le sommet.

     Dessinée sous cet oeil, plus rien ne serait à voir d’autrement descriptif que l’impression irréfléchie de proportions informulables sans le trait de la géométrie. D’où le dessin qui par sentences refait de nombre par son écrit dans la logique de proportions qui toutes sonnent l’harmonie. Car l’étonnement qui transperçat de quelques mots les faits contés ne perd rien de la beauté plus réelle de Khéops qui dans son plan pris de la face élevée devant l’oeil continu de révéler plus inombrables subtilités.

     Dessin de forme, l’apothème mesure 17,804494 centimètres de haut, 22 pour la base, 11 pour la demi-base et 20,92845 d’hypothénuse. Les deux valeurs de 17,804494 et 20,92845 écrites par leurs entiers mesurent respectivement √317 et √438. L’apothème divisé en 14 unités mesure 1,2717496 pour chacune et 1,6185904 lorsque l’apothème est divisé en 11. Le dessin de la base de la pyramide est le même que précédemment, mais le cercle exinscrit aux trois sommets diffère par la longueur du rayon. Celui-ci mesure 12,304494, valeur approchée définie par la géométrie du dessin. Le centre est situé à 5,5 centimètres de haut suivant l’échelle du dessin, cette valeur étant celle de ((11/3)/(2√2)) + (11/3). La vérification par le triangle de base 11 et de hauteur 5,5 donne 12,29837390 pour résultat avec une différence de 0,0061199347 centimètres qui représentent 6,41136021 mètres à l’échelle de la pyramide. Pour éviter cette importante différence, il aurait fallut que le centre du cercle soit situé à 5,5042284 centimètres de haut pour que le rayon mesure 12,300265, valeurs indémontrables par la géométrie.

     Le centre du cercle exinscrit aux sommets de la pyramide lorsque la hauteur mesure 14 est de 2,6756387 centimètres suivant la géométrie du dessin et 2,6785714 par le calcul. Le rayon du cercle mesure (14 – 2,6785714) = 11,321429 centimètres. Cette valeur multipliée par π/2 est proche de la hauteur d’apothème à 0,0136771 près . Si l’on compare ces valeurs à celles de l’apothème, il est à constater que le cercle dont le quart de périmètre est √317 mesure 11,33013240 de rayon, le périmètre complet mesure 71,21797530 soit la somme des quatre hauteurs d’apothème. Le périmètre mesure 44ϕ et le rayon 7ϕ, valeurs comparables à ((308 / 7) x ϕ) = 71,21797760. La hauteur de la pyramide divisée par 7 et multipliée par ϕ est égale à 4 hauteurs d’apothème. Quatre hauteurs d’apothème divisées par ϕ donnent la valeur de 44, soit le périmètre d’un cercle de rayon 7 dont la géométrie s’exprime par le dessin.

     La hauteur de la pyramide mesure 308, cette valeur divisée par 14 donne l’unité égale à 1 lorsque la hauteur est de 14 sur le dessin. Lorsque l’on dessine le triangle de base 1 et de hauteur 1,272727, l’hypothénuse mesure 1,6185904. Cette valeur divise la hauteur de l’apothème en 11 unités lorsque celui-ci mesure √317. Le cercle de rayon 7ϕ mesure 22ϕ sur le demi-périmètre, soit deux fois la hauteur de l’apothème. En vraie grandeur, la valeur de 1,6185904 coudées est contenue 242 fois. Exprimée en mètres, la valeur de 1,6185904 mètres est contenue ((110/3) x π) dans la hauteur de 186,52328 mètres.

     Lorsque l’on divise la hauteur de l’apothème en 7 unités, multipliées par 2 puis divisées par ϕ, la valeur est celle de π exprimées par la longueur du côté d’un carré du dessin du nombre d’or. Cette valeur est celle de la projection verticale de 2 unités portées de l’apothème sur la base du triangle de hauteur 14 dont l’hypothénuse mesure √317.

     De même, si l’on divise la hauteur de l’apothème par 11, la valeur de l’unité mesure ϕ = 1,6185904. Cette unité divisée par 11 et multipliée par la hauteur de l’apothème est égale à ϕ² Lorsque l’on divise ϕ² par 11 et que l’on multiplie par la hauteur de l’apothème, on obtient ϕ³, et ce jusqu’à l’infini de (ϕn / 11) x √317 = ϕ(n + 1). La puissance de ϕ approchée de √317 est ϕ⁶ = 17,981324 supérieur à 17,804494 de 0,1768301 unités. La mesure de l’apothème étant 11ϕ et ce quelle que soit l’échelle du dessin, une unité de ϕ/11 multipliée par 11ϕ est égale au carré de ϕ.

     Si les proportions de la pyramide n’expriment que la valeur de π inscrite de logique dans la numération des nombres, les proportions de l’apothème sont essentiellement dessinées par le nombre d’or dont la composition est de moitié celle de la base, créant ainsi une harmonie qui par l’évidence, mystifia l’impression sensorielle des plus habiles observateurs. Architecture en trompe-l’oeil, la pyramide n’eut de géométrie que par le nombre arrêté de mesures qui parvinrent à faire montre de vérités, alors traduisibles en dessins.

     Dessins de voyages, d’explorations en terres sacrées, dessins architectes des regards portés vers l’orient, dessins géomètres faisant oeuvre des classiques par le trait mesuré des lignes les plus essentielles. Les pyramides font galeries de tout le mystère venu de là, déïfiées de couleurs et d’inégalables poésies dans le trait posé au loin des figures éternelles, que l’horizon repeint élève sous les yeux. Masquées de lumières dans l’éblouissement des sables, dorées par le hâle caressant des dunes, ou carrées de fusains faisant noirs sanglots, leur mine émerveille le pélerin des sables qui par là rejoint les origines de la vie.

     Mortifiées de propos et sauvages fourberies, les pyramides continuent pourtant de faire vies de l’éveil qui embaume les sens du discret sentiment d’être devant le fait d’une omniscience originelle. Métamorphose de l’homme, les pyramides font absence de cette physionomie cependant grandie de la force colossale qu’il fallut dresser dans l’ombre solaire pour accomplir les deux lignes du dessin d’un nombre, arrondi de faîte par un seul trait. La courbe fait voûte imagée aux siècles d’emerveillements sans mots pour extrapôler le sentiment incalculable d’une beauté infinie, mais sobrement volubile, qui rend marri le narrateur de cet hypèthre pharaonique.

     Sans doute fallut-il épitaphes funèbres pour conter les merveilles de coeurs asservis à l’austérité d’une architecture sans autre pareille fantaisie. La science a bâti le nombre par instinctives confrontations de l’être pyramidal à l’être savoir humain, par discernement du corps et clairvoyance de l’esprit façonné de passions sensiblement domptées. “Il y a plus de choses sur la terre et dans le ciel qu’il n’en est rêvé dans la philosophie” instruit de cette vérité là, sans l’équivoque passive de vouloirs fallacieux empressés de livrer déductions surfaites.

     Nombres et nombres de dires et de voirs parcourrus jusqu’à l’Antiquité n’auraient d’intérêt sans la vraissemblance d’un mystère authentique témoignant des sciences primitives d’une humanité formulée des savoir lithiques abondants par la piété. Sagesse bâtie avec son peuple, la pyramide est le tableau commensurable de réflexions abouties par le fondement des nombres d’oeuvre à faire le cercle d’une quadrature triangulée, plus grande en proportions de cet immense qualité qui met secrets en chaques mesures des plus désuets procédés. S’il eût fallu une raison de bâtir, le gigantisme et le nombre en justifient la volonté de graver pierres polies éternellement figées dans les sables.

Lieu du site	Angle de la pyramide suivant J.P. Lauer	Proportions déduites	Dimentions restituées en coudées de 0,5238095 mètres.	Rapport de la demi-base sur la demi-hauteur.	Commentaires
Meïdoun, revêtement final dû à Snéfrou.	51°50’35”51°84’27”73”’360 / 51°84’27”73”’ = 6,944073.	14 / 11	Base = 280Hauteur théorique = 178,18	1,5714446 ≈ π / 2	Pour que les proportions soient de π/2, il faut que la hauteur mesure 178,181818.
Snéfrou à Dahchour:
Dahchour Sud, tronçon supérieur de la rhomboïdale.	54°27’44”54°46’23”22”’360 / 54°46’23”22”’ = 6,6100744	7 / 5	Base = 350Hauteur théorique = 245	1,4285714	Ce rapport de proportions est de 10π/22. L’angle d’inclinaison de la pyramide correspond à un cercle divisé en 6,666666 secteurs égaux. Cette régulation a donc une géométrie.
Tronçon supérieur de Dahchour Nord.	43°22′43°36’34”22”’360 / 43°36’34”22”’ = 8,3019278	17 / 18	Base = 420Hauteur théorique = 198,33	2,1176471
Petite pyramide satelite de la rhomboïdale.	50°11’40”50°19’44”29”’360 / 50°19’44”29”’ = 7,1721107	6 / 5	Base = 100Hauteur théorique = 60	1,666666	Cette valeur est égale à 5 / 3, soit le demi-périmètre d’un cercle de 1,590909 avec π = 3,14285714
Khéops.	51°50’35”51°84’27”73”’	14 / 11	Base = 440Hauteur théorique = 280	1,57142857	Les proportions de Khéops sont π/2 fois plus grandes que celles de Meïdoun.
Khéphren à Guizeh.	53°7’48”53°13’01”02”’360 / 53°13’01”02”’ = 6,7758199	4 / 3	Base = 410Hauteur théorique = 273,33	1,5	La demi-base divisée par trois est comptée quatre fois en hauteur.
Mykérinos à Guizeh.	51°20’25”51°34’01”92”’360 / 51°34’01”92”’ = 7,0120501	5 / 4	Base = 200Hauteur théorique = 125	1,6
Ouserkaf à Saqqarah.	53°7’48”53°13’01”02”’	4 / 3	Base = 140Hauteur théorique = 93,33	1,5	Les proportions sont (41/44)π fois inférieures à celles de Khéphren.
Sahourê à Abousir.	50°11’40”50°19’44”29”’	6 / 5	Base = 150Hauteur théorique = 90	1,666666	Les proportions sont 1,5 fois plus grandes que la petite pyramide satelite de la rhomboïdale.
Néferirkarê à Abousir.	53°7’48”53°13’01”02”’	4 / 3	Base = 200Hauteur théorique = 133,33	1,5	Les proportions sont 2,05 fois inférieures à celles de Khéphren et 10π/22 fois plus grandes que celles d’Ouserkaf.
Néouser-rê à Abousir.	51°50’35”51°84’27”73”’	14 / 11	Base = 155Hauteur théorique = 98,64	1,5713706 ≈ π/2	Si la hauteur avait mesuré 98,636363, le rapport aurait été de π/2. Les proportions de Néouser-rê sont 2,8387097 fois inférieures à celles de Khéops
Isési-Djedkarê à Saqqarah.	53°7’48”53°13’01”02”’	4 / 3	Base = 150Hauteur théorique = 100	1,5	La pyramide de Isési-Djedkarê est 2,733333 fois plus petite que celle de Khéphren.
Ounas à Saqqarah.	56°18’35”56°30’99”32”’360 / 56°30’99”32”’ = 6,3931883	3 / 2	Base = 110Hauteur théorique = 82,50	1,333333	Cette proportion correspond au tier d’un demi-cercle de périmètre 4. De même, 2,733333 est le tier de 8,2, proportion rappelant celle de la hauteur d’Ounas.
Les quatres pyramides de Saqqarah: Téti, Pépi 1er, Mérenrê, Pépi II.	53°7’48”53°13’01”02”’	4 / 3	Base 150Hauteur théorique = 100	1,5	Ces proportions sont identiques à celles de Isési-Djedkarê à Saqqarah. Ces porportions sont 15π/44 fois celles d’Ouserkaf.
Amenemhat Ier à Licht.	54°27’44” = angle supérieur de la rhomboïdale	7 / 5	Base = 150Hauteur théorique = 105	1,4285714	Ce rapport de proportions est de 10π/22, identique à celui de Dahchour Sud.
Sésostris Ier à Licht.	49°23’55”49°39’87”04”’360 / 49°39’87”04”’ = 7,2876406	7 / 6	Base = 200Hauteur théorique = 116,66	1,7142858	Ce rapport de proportions est de 12π/22.
Sésostris III à Dahchour.	56°18’35”56°30’99”32”’	3 / 2	Base = 200Hauteur théorique = 150	1,333333	Ces proportions sont 1,818181 fois plus grandes que celles d’Ounas soit (10/7) x (4/π) = (10π/22) x (4/π)
Amenemhat III à Dahchour	57°15’50”57°26’47”73”’360 / 57°26’47”73”’ = 6,2865874 = π x 2,0002778 ou π = 3,1432937	14 / 9	Base = 200Hauteur théorique = 155,55	1,2857143	Ces proportions sont de 9π/22 = 2π – 5

     L’opulente diversité des nombres sous une même écriture met en question tout ce que le savoir a pu élaborer de connaissances depuis Khéops jusqu’à Alexandrie, puis la Grèce jusqu’aux modernes, au regret de ne voir ailleurs aucune évidente similtude qui fasse principe de cette géométrie. Appliquée par l’édifice, la géométrie de Khéops semble grandie d’une maturation anciennement étudiée et par suite mise au secret de ses uniques concepteurs. Peut-être faut-il y voir l’accomplissement d’une théorie qui parvint à faire l’ouvrage postume d’un Imhotep, étudié et refondé dans le dessin substanciel des pyramides de Meïdoun et l’unique Grand Monument du complexe de Guizeh.

     L’histoire méconnue des fondations du nombre π, son extinction par la suite de toutes évidences imméiates laissent à tort déductions de penser que Khéops fut le seul monument de ce nombre. Si l’on compare les nombres de la géométrie à ceux connus des autres pyramides, les proportions différemment inclinées montrent semblable intention du cercle. Dans le Mystère des Pyramides, J.P. Lauer indique pages 258 et 259 de son ouvrage, les proportions des pyramides les plus importantes sur lesquelles les commentaires peuvent laisser à prévoir d’autres régulations toutes aussi prenantes.

     Les angles indiqués en italique dans le tableau sont ceux recalculés suivant les proportions de la base et de la hauteur. Pour Meïdoun, Khéops,  et Néouser-rê l’angle est de 51°84’27”73”’, pour le tronçon supérieur de la romboïdale et la pyramide d’Amenemhat Ier l’angle est de 54°46’23”22”’, pour le tronçon supérieur de Dahchour Nord l’angle est de 43°36’34”22”’, pour la petite pyramide satelite de la rhomboïdale et la pyramide de Sahourê, l’angle est de 50°19’44”29”’, pour les pyramides de Khéphren, Ouserkaf, Néferirkarê, Isési- Djedkarê, les quatre pyramides de Téti Ier, Mérenrê et
Pépi II, l’angle est de 53°13’01”02”’, pour la pyramide de Mykérinos l’angle est de 51°34’01”92”’, celui d’Ounas est de 56°30’99”32”’, celui de Sésostris Ier de 49°39’87”04”’, celui de Sésostris III de 56°30’99”32”’ et celui de Amenemhat III de 57°26’47”73”’.

Les pyramides de la IVème dynastie:

Meïdoun, La rhomboïdale de Dahchour, Khéops, Khéphren, Mykérinos, Ouzerkaf.

Les pyramides de la Vème dynastie:

Sahourê, Néferirkarê, Néouser-rê, Isési-Djedkarê, Ounas.

Les pyramides de la VIème dynastie:

Téti, Pépi Ier, Mérenrê, Pépi II.

Les pyramides de la XIIème dynastie

Amenemhat Ier, Sésostris Ier, Sésostris III, Amenemhat III.

     Il semble d’évidence démontrée que toutes les pyramides présentent la même intention de construire suivant les connaissances fondées sur la géométrie du cercle et probablement suivant un rapport constant de la valeur de π dont le périmètre de 44 unités est multiple des 7 unités du rayon. Il faut pour cela remarquer les valeurs qui définissent les mesures de la base et de la hauteur de chacune de ces pyramides, la base étant constamment écrite de nombres entiers alors que ceux définissant la hauteur sont des nombres décimaux, particuliers dans la répétition du même chiffre après la virgule. Propriété du mode de calcul égyptien, toutes les hauteurs sont des fractions d’une unité plus grande par 3, 6, 7, ou 11.

     A Meïdoun comme à Khéops et Néouser-rê, la hauteur multipliée par 11 est égale à 7 fois la longueur de la base. Pour le tronçon supérieur de Dahchour Nord, 18 fois la hauteur mesure 8,5 longueurs de base. Pour la pyramide de Khéphren, trois fois la hauteur vaut 2 longueurs de base, de même qu’à Ouserkaf et Néferirkarê. A Ounas, 4 hauteurs de la pyramide valent 3 longueurs de base. Pour la pyramide de Sésostris Ier, 6 fois la hauteur vaut 3,5 fois la longueur de la base. Il est donc faux de penser que Khéops ait pu être la seule pyramide fondée sur la géométrie du nombre π, l’ensemble des valeurs indiquées dans le tableau étant toutes significatives d’un dessin impliquant le tracé du cercle.

     Peut-être faut-il comprendre ici la signification mystique du cercle lié de nature à tout ce qui environne l’horizon humain. De forme trop arrondie pour conforter l’architecture, le cercle a toujours été un symbole matriciel des rigueurs imposées aux comportements quotidiens, droits par nécessité quand l’esprit fait la ronde des alégories de coutumes infléchies en morales. L’intimé sans doute de l’agoraphilie fut le cercle dans sa plus secrète nature, édifiant de la nimbe lumineuse du nombre l’harmonie du cercle dans le carré.

     Quadrature parfaite de la ligne asymptote à son centre imagé fesant le sommet, la pyramide égyptienne est l’astre féerique de tout les savoirs de la géométrie. Et par-là faut-il à nouveau rappeler que les connaissances restent à devoir faire sciences démontrées, car il n’y a de vérité dans le carré d’un cercle que par l’équation de sa racine. Expression de surface d’un nombre entier, la racine détermine la longueur du côté produit par mesures des diagonales rayonnantes d’un carré déroulé sur son unité. Expression de l’aire d’un nombre décimal, la racine n’est plus qu’une approximation de séries relatives d’unités comptées pour réduire le nombre à plus simple expression.

     La raison qui met en volume l’espace de toutes les pyramides de l’ancienne Egypte est sans doute tributaire d’une géométrie qui prend racine par la surface. Ronde comme tous les entiers qui définissent la base, l’unité multiplie seulement la racine de deux en proportions d’égale valence à celles définies par le dimensionnement. L’ampleur des côtés qui font la base impose que rigueur fasse chantier, par la racine pour trianguler chaque surface en nombres d’entiers. Multiples de 1 pour les parallèles, de √2 pour les diagonales, ces mesures tracées par la ligne d’un cercle n’accomplissent qu’un geste par le compas.

     Si l’étude des dimensions de toutes les pyramides de la Vallée des Rois laisse présumer une géométrie conçue dans le dimensionnement de la base, la pyramide de Khéops démontre différemment l’élaboration d’une géométrie de l’espace faisant compte des dimmensions du plan proportionnées par l’élévation. La hauteur de Khéops est le rayon d’un cercle dont le périmètre mesure celui de la base, prouesse de l’esprit qui réalisa la quadrature parfaite de tous les nombres.

     Le cercle dessiné par la hauteur de Khéops mesure quatre longueurs de la base de la pyramide. La courbe étirée en carré est inscrite dans un cercle de diamètre la diagonale de la pyramide dont la proportion du rayon est (π x √2) / 4, soit la hauteur multipliée par π√2 pour mesurer le périmètre du cercle. Le rayon de longueur 342,23968 coudées de 0,4761904 mètres mesure 11 unités de la demi-base multipliées par la √2 de la diagonale d’une unité carrée. Cette triangulation indéformable du carré divisé en deux triangles isocèles égaux permet le tracé d’une géométrie plane constructible par l’unité.

     Lorsque l’on divise la coupe diagonale de la pyramide par chacune de ces unités, la hauteur mesure 14 unités de longueur 1 et la base 11 unités de √2, multiples de l’unité par la diadonale du carré de côté 1. L’élévation du triangle mesure √438 d’hypothénuse, divisible en 11 unités de longueur 1,9025863. La projection de l’unité de l’arête sur la hauteur de la pyramide mesure 4/π, inscriptible 11 fois dans la longueur de 14. Chacune de ces unités définissent avec le nombre d’or la récurence parfaite de ϕ, ϕ+1, ϕ+2, et
ϕ+n par le carré de chaque racine des nombres entiers lorsque ϕ = (4/π)²

     S’il est improbable que les architectes de l’ancienne Egypte aient eu conscience de toutes les particularités remarquables des racines carrées pour proportionner les aires de chaque carrés d’unités entières, il est sans doute moins certains qu’ils en aient ignoré le fonctionnement défini plus tard dans le théorème de Pythagore. “Dans un triangle rectangle, le carré construit sur l’hypothénuse est équivalent à la somme des carrés construits sur les autres côtés” énonce la formulation d’un phénomène constant de la nature des formes, qui du triangle au carré équilibre les nombres dans la géométrie du cercle.

     Propriété particulière de la géométrie plane, le théorème appliqué aux volumes suit également cette logique de nombres inscrits dans le dessin des formes quadraturées sur l’unité. Dans le volume de quatre cubes, toutes les racines de 1 à 9 sont construites point par point dans le tracé des diagonales proportionnées sur l’unité dont la longueur du côté mesure 1. Le carré de chaque racine est multiple du carré de 1 et le carré des proportions fait le carré de chaque racine. Ainsi √3/√2 étant égal à 1,2247449, cette valeur au carré est égale à 3/2. De même, 9/2 étant égal à 4,5, la racine de cette valeur est égale √9/√2. Toutes ces propriétés définissent la géométrie de l’espace mesuré par contenance de chaque superficie.

     Arpenteurs expérimentés, les égyptiens connaissaient de pratique toutes les géométries simples permettant d’établir par le trait les calculs les plus compliqués, et sans doute autant oeuvrables qu’une formulation permet d’établir en nombres transcendants toutes les mesures d’une construction. Les décimales d’un nombre n’ont d’absolue que la limite d’un trait dont l’épaisseur fait pointillés des chiffres après la virgule, arrondis par entités concrêtes dans le tracé de l’harmonie qui régule les mesures de la géométrie.

     Construire par le dessin ce qui ne peut être calculé façonne par le geste la juste proportion des nombres que l’intuitive réalisation permet de démontrer par la fréquence des résultats venus à s’affirmer. De l’hypohèse observée de rigueur, le théorème par nécessité définit une formulation explicite de moyens pour parvenir à un résultat qui par principe d’une méthode permet de construire la géométrie dont le dessin fait le calcul. Les tables d’un nomogramme s’inscrivent dans le dessin de toutes les formes simples de la géométrie, lorsque de l’unité, chaque mesure permet de compter les proportions réalisables par transcription de lignes.

     Si l’évidence semble acquise par connaissance des faits remarquables, il est pourtant moins immédiat d’en mesurer l’exactitude lorsqu’à différentes échelles, les nombres se multiplient par toutes les décimales inconnues de la géométrie. Parmis ces nombres irrationnels qui trouvent place dans le dessin se trouvent les plus complexes indémontrables par le compas. Les racines des nombres font géométrie d’un simple carré qui a l’inverse n’a de racine que par procession de calculs dont l’approximation incite à résolution de définir une règle méthodique qui permette des rapprochements.

     Comment diviser un nombre pour que le résultat soit le dénominateur dont la surface du carré mesure l’aire du nominateur ? Par rapprochements devrait-on dire, du dessin d’une ligne à la surface d’un rectangle dans lequel chaque triangles se composent en un seul carré. Solution d’un problème de la vie courante qui ne satisfait aucune logique bien que le Papyrus de Berlin atteste de méthodes appliquées par l’Egypte Antique pour résoudre l’arithmographie.

     Si l’arithmétique énonce des problèmes souvent contournables dans la réalité pratique de tous les jours, il n’est pas moins certain que la définition d’une méthode pour résoudre la formulation des racines carrées a dû s’imposer très tôt pour affirmer de rigueur tous les dessins de la géométrie. La quadrature du cercle en montre l’évidente nécessité de pouvoir définir deux formes dont l’aire contient le même nombre de mesures dans le carré construit sur le rayon du cercle et celui proportionné par la valeur de π.

     Lorsque l’on dessine à grande échelle le rayon du cercle de longueur 7, que l’on divise chaque unité de longueur 1 en 20 unités plus petites, chacune de ces unités mesure 2 millimètres pour un rayon de 28 centimètres. Connaissant la longueur du segment de 20 unités porté sur le périmètre du cercle, on peut par triangulations, déterminer la longueur d’un segment d’un vingtième d’unité. Ce segment mesure 0,200254633 centimètres, valeur inférieure à celle de l’arc de cercle. La longueur de ce segment multipliée par le nombre de divisions portées sur le périmètre du cercle permet de mesurer le périmètre complet du polygone de 880 côtés. Lorsque le cercle mesure 28 de rayon, le quart de périmètre du polygone mesure 44,05601930 centimètres, soit le périmètre du cercle lorsque le rayon mesure 7. La valeur de π est de 3,14685695 supérieure à 22/7 dans la proportion d’un tracé dont la ligne tend vers la limite voisine de la courbe du cercle. 

     Partant de la longueur de chacun des segments de 0,200254633 centimètres, on peut par suite déterminer l’aire de chaque triangle de la construction dont la somme mesure 2,80789394 cm² pour chaque portion d’un degré du calcul. Similairement à l’opération précédente, il suffit de multiplier cette aire par le nombre des divisions du cercle pour trouver l’aire totale du polygone complet. Cette aire est de 2470,94667 cm² pour le cercle de rayon 28 et 154,389917 pour le cercle de rayon 7. Le carré de surface égale à celle du cercle de rayon 28 mesure 49,70861770 de côté et celui de surface égale à celle du cercle de rayon 7 mesure 12,42537390 centimètres .     Avec π égal 3,14685695, la valeur du degré mesure 0,200254633 centimètres. La longueur du rayon du cercle divisée par cette valeur contient 139,821984 degrés. Avec π égal 3,14159265, le périmètre du cercle mesure 175,929189 centimètres contenant 880 degrés de 1,99919533 millimètres. La longueur du rayon divisée par cette valeur comprend 140,05635 degrés. Il en résulte que quelle que soit la valeur de π, la proportion d’un degré 880 fois plus petit que la longueur du périmètre du cercle est proche du 140ème la longueur du rayon. La valeur supérieure à 140 divise le cercle par

les proportions des polygônes inscrits dont le nombre de côtés est supérieur à 880, et la valeur inférieure à 140 le divise par les proportions de polygônes dont le nombre de côtés est inférieur à 880.

     Les variables en plus ou en moins se fixent cependant à 140 lorsque π vaut 3,14285714 correspondant au nombre de degrés contenus par unités de 20 dans la proportion du rayon de longueur 7. Le périmètre du cercle peut ainsi être divisé en 880 degrés de même valeur que ceux portés sur le rayon. L’étude développée préalablement implique toutefois que logique appliquée suive la règle de division du cercle par multiples de 11 jusqu’à l’unité. Le cercle de 44 unités ainsi redivisé en 22 degrés mesurerait sur le périmètre du cercle 968 degrés au lieu de 880. Le rayon divisé par 7 unités de 22 mesurerait 154 degrés proportionnels au nombre d’unités contenues dans la quadrature du cercle.

     La quadrature d’un cercle est la proportion par laquelle le carré du rayon du cercle doit être multipliée pour dessiner un carré dont l’aire est celle du cercle. La surface du cercle de rayon 28 est proche de celle du polygone dont l’aire mesure 2470,94667 cm². L’aire du polygone divisée par le carré du rayon donne 3,15171769 pour valeur approchée de π. Lorsque le rayon du cercle mesure 7, l’aire du polygone est de 154,39060100 cm² pour une valeur de π de 3,15082859 jusqu’au carré du rayon. Si, pour ajuster le calcul, l’aire de chaque portion de degré avait été calculée sur les divisions du rectangle de longueur 10 degrés et d’épaisseur la plus grande hauteur jusqu’à la courbe du cercle, l’aire du cercle de rayon 28 aurait mesuré 2464 cm² et π = 3,14285714. Il existe donc une valeur de π qui admet le calcul de l’aire d’un cercle lorsque celui-ci est exinscrit à un polygone dont le nombre de côtés est supérieur à celui qui a permis d’établir la valeur de π.

     π détermine une fraction du périmètre sur le diamètre d’un cercle lorsque 7 unités du rayon sont portées 44 fois sur le périmètre. Lorsque les 44 unités sont divisées en 22 degrés déterminant les portions de l’aire d’un cercle, chacune de ces portions agrandies jusqu’à la limite de la courbe déterminent une aire multiple du carré du rayon et de π. Il y a donc quadrature possible et dans la perfection de la valeur de π qui permet à toutes mesures de rester dans la rationnalité.

     La difficulté pourtant, consiste à définir un dessin qui permette de multiplier une aire par la valeur d’un nombre dont seul la racine est quantité mesurable. Pour dessiner la quadrature du cercle de rayon 28, il faut multiplier chacun des côtés du carré de 28 par la racine de π dont on ne connait que le carré. Le propduit de 28 par √π mesure la racine de la quadrature du cercle.

“On ne peut pas, avec l’aide seulement d’une règle et d’un compas, construire un carré dont l’aire est exactement égale à celle d’un cercle (car une telle construction ne peut être traduite sous forme d’une équation algébrique dont π devrait être solution).“

LA RECHERCHE- Hors Série n°2 d’août 1999- p112.

     Déterminer par le dessin les valeurs exactes des racines carrées est exercice infernal sans résultat de satisfaction si l’on ne considère que la règle et le compas comme outils de travail. Pourtant, si l’on imagine dessiner une ellipse par la seule règle et le seul compas, peu de lignes peuvent également prétendre trouver ajustement de rigueur. Il faut pour cela des outils bien plus simples qu’une corde et deux pointes suffisent à satisfaire.      Si l’on raisonne le dessin de la quadrature par les deux foyers multiples par π, les nombres 7 et 22 sont les deux limites entre lesquelles il existe une mesure unique multiple de 7 et de 22 par la racine de π. En dessin, cela revient à dire qu’il existe une droite et une seule perpendiculaire au plan du repère dont chaque extrêmité est coupée par deux droites parallèles entre elles passant par 7 et par 22.

     L’exactitude de la géométrie étant de toute manière improbable, il faut pour satisfaire au dessin, parvenir à définir une méthode de tracé qui elle, sera juste pour permettre par la suite toutes les vérifications mathématiques nécessaires à la définition de la plupart des racines carrées. Sachant qu’il n’existe qu’une droite de l’espace perpendiculaire au plan du repère dont chaque extrêmité est coupée par deux droites parallèles, la ligne brisée qui va d’un point à l’autre est d’abscisse multiple des deux points d’abscisses 7 et 22. La longueur de l’abscisse de cette droite, élevée au carré est également multiple des deux carrés d’abscisses les deux points, marquant ainsi sur la diagonale du repère, trois points de coordonnées proportionnelles aux côtés des carrés. Les trois carrés sont proportionnels entre eux par le carré des proportions qui définissent la longueur de chaque côté des trois carrés et chaque carré trouve dans le cercle coordonnées similaires de proportions.

     Si l’on conçoit qu’une approximation qui est juste vaut mieux qu’une certitude intraçable, une machine pour remonter le temps du dessin jusqu’à la définition du côté du carré démontre, si la machine fonctionne, qu’une géométrie peut être tracée à l’aide de règles et de compas articulés sur le plan du dessin. La mise en fonctionnement commence par le calcul du nombre dont on cherche la racine pour le multiplier par 7. Le résultat produit étant multiple du carré de longueur 7 par la valeur du nombre en étude, le carré multiple de 7 est dessiné sur une feuille. Fixée sur le tableau de traçage, la machine aligne les points en déplaçant le té qui articule les règles. Le point B placé dans l’alignement de D, la racine du nombre est ainsi produite lorsqu’on divise par 7 la longueur ainsi obtenue.

     Toutefois, il semble évident que ce procédé ne puisse fonctionner qu’avec des nombres de petites valeurs inscritibles dans le plan d’une feuille sur laquelle opérer le calcul, à moins que par séries de traits, le calcul puisse être autrement effectué. Si l’on considère les nombres de valeur supérieure au plan de la feuille, il faut alors imaginer le chemin qui permettent de les réduire. Le plus cours est celui du cercle dont il est aisé de connaître toutes les valeurs inscrites dans le périmètre et la mesure de l’aire qui le définit.

     Le rayon de 7 étant le prototype le plus immédiat du dessin de π, le carré de √154 est la quadrature la plus immédiate du cercle contenant sur chaque côté 7 unités de √π. Supérieur à ce carré dont le côté mesure 7√π, le carré de 22 est le multiple par 7 et √π. En exemple, si l’on cherche à dessiner la racine de 438, il faut trouver dans l’expression du nombre toutes les valeurs multiples du cercle de rayon 7, pour réduire en valeurs mesurables les fractions de 438. Sachant qu’un cercle de rayon 7 mesure 44 de périmètre, que l’aire mesure 154 unités inscriptibles dans le dessin d’un carré, le nombre 438 est similairement inscriptible dans le dessin d’un cercle dont l’aire est identique au carré de côté la racine du nombre. Si l’on divise 438 par 154, l’aire de chaque unité carrée mesure 2,8441558 et 7 de ces unités mesurent 19,909090. Ces valeurs sont également celles d’une règle de longueur 7 dont la hauteur mesure 2,8441558. Le nombre 7 est multiple de 22 jusqu’à 154, ce qui revient à dire que 438 divisé par 22 est égal à la longueur de 7 unités. Celles-ci mesurent 19,909090, non plus sur une surface, mais la longueur d’un trait 22 fois plus petit qu’une ligne de longueur 438. Cette mesure de 19,909090 est divisible en 7 unités linéaires de longueur 2,8441558. Chaque carré de côté 2,8441558 mesure 8,0892225 de surface, contenu 49 fois dans le carré de côté 19,909090.

     Les deux carrés de 7 et de 19,909090 ainsi définis dans la proportion de 438, il faut trouver le multiple des deux nombres qui puisse être dessiné. Cela revient à chercher la racine de 2,8441558 contenue 7 fois dans le dessin d’un carré proportionnel à 7 et 19,909090. Passé dans la machine à remonter le temps, le dessin permet d’arrêter la mesure d’un carré de longueur 11,805238 de côté contenant 7 unités de 1,68646251 dont le carré mesure 2,8441558. Lorsque l’on dessine la droite passant par 7 et le coin du carré de côté 11,805238, la parallèle à cette droite passant par l’abscisse de √154 coupe la diagonale du repère par l’angle du carré dont l’aire mesure 438. Ce dessin fait le tracé de 11,805238 par √π, et le résultat mesure 20,92844940. Cette valeur élevée au carré mesure 438.

438 /π = 11,805238²

438 / 7π = 19,909090

19,909090 / 7 = 2,844156

7² x 2,844156 = 19,909090²

2,844156 / 0,14285714 = 19,909090

2,844156 x 0,14285714 = 0,4063081 = 2,844156 / 7

0,4063081² = 0,1650863

0,1650863 x 7 = 1,1556043 ≈ 2,844156 – √2,844156

438 x (π/2) = 688,28573 = 11,805238² x 2 x (π²/4)

11,805238² x 2 x (π²/4) x (2/π) = 438

√688,28573 = 26,2352

26,2352 / (π/2) = 16,695127

16,695127 / √2 = 11,805238

(16,695127 x √77) / 7 = √438

(16,695128 x (π/2))² / (π/2) = 438

√438 / √π = 11,805238

11,805238 x √π = √438 = 11,805238 x (π/2) x √(4/π)

438 / π = 139,363636

139,363636 / 1,113636 = 125,14286

(125,14286 / 44) x 7 = 19,909090

     Avec un autre nombre, si l’on cherche la racine de 586, il suffit de diviser 586 par 22, dessiner le carré sur une feuille, placer le carré de 7 à l’origine du repère et passer le calcul dans la machine à remonter le temps. Une droite verticale d’abscisse 13,654836 permet ainsi de dessiner 7 racines de (586 / 22 )/7 soit √(26,636363 / 7) qui mesure 1,9506909. La feuille placée sous la machine, le carré de √154 est dessiné par 7 et 22. La parallèle de la droite passant par 7 et le coin du carré de côté 13,654836 est tracée sur l’abscisse de √154 jusqu’au point d’intersection avec la diagonale du repère. L’angle du carré ainsi obtenu mesure 24,207437 de côté et l’aire 586.

586 / 22 = 26,636363

26,636363 / 7 = 3,8051948

586 / π = 186,454545 = 7 x 26,636363 = 13,654836²

3,8051948 / 3,8051948² = 0,2627986 = 1 / 3,8051948

√3,8051948 / 0,2627986 = 7,4227787

0,2627986 x 7 = 1,8395902 = 7 / 3,8051948

26,636363 / 7,4227787 = 3,5884723

7 / 3,5884723 = 1,9506908 = √3,8051947

7 x 1,9506908 = 13,654836

13,654836 x 1,9506908 = 26,636363

13,654836 / 1,8395904 = 7,4227565

7,4227565 = 1,95069083

3,5884723 / 0,2627986 = 13,654838

12,877133 = 7 x 1,8395904

12,877133 = 3,5884723²

26,636363² / 12,877133 = 7,4227787²

“L’idée de “quarrer” le cercle, c’est-à-dire de construire, à la règle et au compas si possible, un carré de même aire qu’un cercle donné, tracassait déjà les anciens. Ce fameux problème de la quadrature du cercle a pendant vingt-trois siècles empêché de dormir plus d’un mathématicien. Hippocrate de Chio était bien arrivé, dès le Vème siècle avant J-C, à quarrer quelques “lunules”, figures composées d’arcs de cercles. De nombreux “géomètres” s’y sont par la suite employés, dont Léonard de Vinci, qui en dessina, dit-on, une centaine. Tous ont eu ainsi l’impression de faire un bout de chemin vers la résolution du problème historique. La question a été définitivement close en 1882 quand Lindemann, prouvant la transcendance de π, a du même coup prouvé l’impossibilité de la quadrature du cercle.“

LA RECHERCHE- Hors Série n°2 d’août 1999- p119

     Je ne sais quel est le chemin accompli jusqu’ici, mais il est évident que le cercle n’est pas infini, que par là il peut être mesuré, que plusieurs cercles peuvent être comparables et qu’alors la transcendance n’existe plus dans le fait qu’une droite verticale et une seule coupe les deux parallèles définies par les limites extrêmes de deux nombres, l’un étant le rayon, l’autre le périmètre du demi-cercle. Par le fait de la “machine à remonter le temps”, il est évident qu’un dessin existe pour définir par la géométrie la méthode de tracé qui partant de deux points permet de trouver la mesure commune qui multiplie ou divise les points d’extrême limite.

     Après avoir démontré que la racine du carré d’aire la surface du cercle pouvait être calculée sur le dessin de deux carrés, l’un étant le carré du rayon et l’autre le carré du demi-périmètre, l’étude de la racine carrée de 438 et de 586, nécessite de rappeler la signification de chaque valeur. Ces deux nombres, par hypothèse, représentent l’aire d’un cercle dont on ne connait le dessin qu’après réduction de ces nombres par la division en 22, puis 7 unités pour déterminer le dessin de deux carrés. L’un est constant à tous les calculs, l’autre variable suivant la valeur du nombre dont le dessin détermine la racine.

     Le carré multiple de 7 et celui de la division par 22 déterminent l’aire du carré dont le côté est le rayon d’un cercle, qui, multiplié par √π permet d’obtenir la racine du nombre en étude. Cela revient à dire que le carré multiple de 7 détermine le rayon du cercle dont l’aire du carré multipliée par π est égale à l’aire du cercle dont on cherche la racine carrée. Lorsque le rayon du cercle mesure 11,805238, l’aire du cercle mesure 438, valeur multiple du demi-périmètre du cercle par la valeur de √π. Si l’on divise 11,805238 par 7 que l’on multiplie par 22, que l’on divise le résultat obtenu de 37,102177 par √π, on obtient la valeur de la racine du carré dont l’aire mesure 438. Avec 586, le résultat est le même qu’avec tous les autres nombres. Le rayon du cercle divisé par 7 multiplié par 22 puis divisé par √π est égal à la racine du nombre dont on connait le carré.

     De l’ensemble de ces résultats, il est alors possible d’énoncer toutes les règles essentielles qui définissent le cercle et la quadrature dont l’aire carrée est celle du cercle. Le carré du demi-périmètre d’un cercle est π fois plus grand que le carré dont l’aire est celle du cercle, et le carré dont l’aire est celle du cercle est π fois plus grand que le carré du rayon. Du carré le plus grand au carré le plus petit, il existe une droite et une seule qui coupe le plan des abscisses par une verticale dont chaque extrêmité détermine deux droites parallèles entre elles. Les projections verticales de chacun des carrés se rejoingnent par des arcs de cercles dont le centre est l’origine du repère, par une droite et une seule de l’espace dont l’angle fait 55°66’18”43”’. Cette droite est dans l’espace l’unique règle par laquelle toutes les racines et carrés de π sont dessinés par projection.

     L’aire du cercle est le carré du rayon multiplié par π. L’écriture mathématique est πr² que la fraction de 22r²/7 permet de dessiner par la géométrie. La quadrature du cercle est √(22r² / 7), soit le carré du demi-périmètre divisé π, ou le carré du rayon multiplié par π suivant les différentes données du calcul. Pour déterminer la racine de la quadrature du cercle il suffit de multiplier 7 fois le demi-périmètre du cercle divisé par √154, ou multiplier la longueur du rayon par √π. La racine du carré de la quadrature du cercle divisée par 22 et multipliée par 7√π est égale à la longueur du rayon du cercle.

     Le rayon du cercle mesure le côté du carré de la quadrature multiplié par 7√π et divisé par 22. Inversement, le côté du carré de la quadrature vaut la longueur du rayon multipliée par 22 et divisée par 7√π. L’aire du carré de la quadrature multipliée par 14/11 est égale au carré du diamètre du cercle. L’aire du carré de la quadrature divisée par 22 mesure 7 carrés de l’unité du rayon. Le côté du carré dont l’aire est celle du cercle multiplié par √(4/π) est égal au diamètre du cercle. Inversement, le diamètre du cercle divisé par √(4/π) est égal au côté du carré. La valeur de √(4/π) est la racine du diamètre du cercle sur le quart de son périmètre soit √(14/11).     Toutes ces valeurs trouvent dans la fondation de Khéops une signification exponentielle lorsque l’on compare entre elles toutes les mesures de sa construction. L’aire de la base est 484² soit 234256 carrés d’une coudée de 0,4761904 mètres. L’aire de l’apothème est de 391,69886 par 242 soit 94791,125. L’aire de la section méridienne est de 308 par 242 soit 74536 et l’aire de la section diagonale est de 342,23968 par 308 soit 105409,82 coudées carrées. L’aire de la base divisée par celle de l’apothème est égale à 14π / 11ϕ. L’aire de la base divisée par celle de la section méridienne est égale à π. L’aire de la base divisée par celle de la section diagonale est π / √2. L’aire de l’apothème divisée par la section méridienne est égale à 11ϕ / 14 ce qui équivaut à l’aire de l’apothème divisée par sa hauteur sur 14. L’aire de la section diagonale divisée par l’aire de l’apothème est égale à 14√2 / 11ϕ. L’aire de la section diagonale divisée par l’aire de 

la section méridienne est égale à √2. L’aire de l’apothème multipliée par 4 et divisée par l’aire de la base est égale à ϕ = 1,6185904 et l’aire de la diagonale multipliée par 4 divisée par l’aire de la base est égale à 14√2 / 11.

     La hauteur de la pyramide mesure 308 ce qui équivaut à 154 x 2. Le côté de la base mesure 484 soit 22 au carré, et le demi-côté de la base mesure 242 soit (11 x √2)². La hauteur de la pyramide mesure 7² x 2π et le côté de la base 7² x π². Le cercle dont l’aire est celle de la base de la pyramide mesure 273,01282 de rayon soit la hauteur de la pyramide divisée par √(4/π). Le rayon de ce cercle divisé par √(4/π) mesure le demi-côté de la base soit 242. Le rayon du cercle multiplié par √π mesure 484 et le rayon du cercle divisé par √π mesure 154. La valeur de 154 est comprise 484 fois dans l’aire de la section méridienne, 484π fois dans l’aire de la base, 121ϕπ fois dans l’aire de l’apothème et 484√2 fois dans l’aire de la section diagonale. L’aire de la base divisée par π² est égale à 14² x 11². Le carré de l’apothème mesure 307,88167 de côté, celui de la section méridienne 273,01282 et celui de la diagonale 324,66879. La proportion de 324,66879 à 273,01282 est de ²√2, celle de 324,66879 à 307,88167 est de √(14√2 / 11ϕ) et celle de 484 à 324,66879 de √(π / √2). La proportion de 484 à 273,01282 est de √π, le carré de la section méridienne étant le rayon carré du cercle dont l’aire mesure 484². La proportion de 484 à 307,88167 est de √(14π / 11ϕ) et celle de 307,88167 à 273,01282 est de
√(11ϕ / 14).

     L’ensemble de ces résultats n’est compatible qu’avec une seule valeur de la coudée dont la mesure est de 0,4761904 mètres, peu conventionnelle aux proportions généralement connues, mais de logique inscrite dans une géomètrie dont l’échelle humaine implique raison de pouvoir compter toutes les mesures. De la plus petite à la plus grande, chaque valeur est proportionnée suivant un ordre constant des nombres utilement mémorisables pour parvenir à faire dessin d’une géométrie savante, évolutive mais facilement praticable dans le dessin de quelques traits.     Savoir, mesurer, connaître. Cette géométrie permet tous les calculs mathématiques de l’addition, la soustraction, la division et la multiplication, jusqu’à résolution plus abstraite des équations du second degré sur la valeur d’un seul nombre, celui de la racine de π. Connaissant son mystère, tout peut être résolu jusqu’au dessin infini de tous les nombres terrestres, lorsque leurs limites sont les mesures entières d’un chiffre après l’autre sans fraction de virgules.

     Sachant opérer par le dessin tous les modes de calculs essentiels à la résolution des opérations courantes, reste pourtant l’interrogation manifeste de pouvoir résoudre les racines carrées autrement que par une machine dont on ne peut prouver le réel fonctionnement. S’il est possible de démontrer par la géométrie la plupart des règles qui définissent l’espace plan du cercle et du carré, il semble indéniable que l’évidence puisse démontrer autrement une géométrie dans laquelle le dessin du cercle puisse aboutir à celui d’un carré.

     Reprenant toutes les démonstrations préalables, il est alors nécessaire de rappeler le naturel de la géométrie, qui par procession de nombres, dessine invariablement les mêmes formulations du dessin, tracé de logique par l’ensemble des modes de calcul courant. L’addition, la soustraction, la division et la multiplication sont des propriétés remarquables de la géométrie auxquelles on peut ajouter la possibilité d’élever un nombre au carré. On sait construire une mesure et la comparer à une autre de telle sorte que la construction de l’espace puisse formuler un résultat, direct ou implicite par le tracé d’un raisonnement.

     Reprenant ainsi la plupart des relations connues pour à mettre en équation le dessin d’un carré il faut parvenir à définir par les nombres le sens donné à chaque valeur. Le rayon d’un cercle définit une longueur facilement mesurable du centre au périmètre. Le carré du rayon définit une aire seulement mesurable sur la longueur d’un côté. La valeur de π détermine un ratio reproduisant le rayon sur le périmètre d’un demi-cercle compté deux fois sur le périmètre complet. Ce ratio multiplié à l’aire d’un carré, reproduit similairement la valeur d’un nombre en autant d’unités carrées que π peut en contenir.

     Lorsque l’unité du rayon mesure 1, l’unité portée sur le périmètre du cercle mesure 3,14285714 comprise 7 fois sur la ligne du cercle. Pareillement, lorsqu’une unité carrée de la quadrature du rayon mesure 1, cette unité est produite 3,14285714 fois par chaque unité carrée de la quadrature du cercle. Ce ratio synonyme de π exprime un nombre composé d’unités de 1, de 2, et les décimales de π.

     Le carré de 1 est dessiné par le rayon du cercle, celui de deux par la diagonale du carré dont la longueur élevée au carré est égale au double du carré de base. Restent alors les décimales de π définies par 1 que l’on divise par 7. Le carré de 1 comprenant 49 unités carrées, la fraction par 7 arrive à 7 pour l’aire d’un carré dont le côté mesure √7. Suivant le théorème de Pythagore, √7 est inscriptible dans le dessin d’un triangle dont la somme des carrés de deux côtés est égale au carré de l’hypothénuse. Si le carré de l’hypothénuse mesure 16 et le carré d’un côté du triangle 9, l’aire du carré de l’autre côté mesure par soustraction 7 unités carrées. Connaissant la racine de 16 et la racine de 9, la triangulation par le compas permet de dessiner la racine de 7.

     La construction du dessin consiste alors à mettre en pratique la définition du théorème pour dessiner d’abord un carré du double celui du rayon, puis un carré construit sur le rayon auquel on ajoute les unités carrées des valeurs exprimées par les décimales de π. Ce carré ayant une aire de 7 unitées ajoutée à l’aire du carré de 49, un autre carré peut être dessiné lorsque deux côtés d’un triangle mesurent les côtés des deux carrés. L’hypothènuse permet ainsi de dessiner un quatrième carré dont l’aire mesure
(7² x 1,14285714). Ce carré ajouté au carré dont l’aire mesure 2 aboutit au dessin de la quadrature du cercle dont l’aire mesure (2 x 7²) + (7² x 1,14285714). Le côté du carré mesure √((2 x 7²) + (7² x 1,14285714)) dont l’équation de la quadrature est:

2x² + x² + (π/22)x² = y²

L’inconnu “y” mesure le côté du carré et l’inconnu “x” mesure le rayon du cercle.

Avec x =7

y² = (2 x 7²) + 7² + ((1/7) x 7²) = 154

y = √154

Avec y = √438

438 = 2x² + x² + (π/22)x²

x = √((438 x 22 / (66 + π)) = 11,805238

     Différemment des solutions algébriques pour définir la racine du carré d’un cercle, c’est ici la géométrie qui permet d’en établir l’équation pour approcher par mesures successives les valeurs réelles de chaque inconnue. Sachant que la quadrature d’un cercle de rayon 7 peut être dessinée, et sachant que tous les nombres sont également inscriptibles dans le dessin du cercle, il devient alors possible d’établir le dessin de toutes les racines carrées. La vérification algébrique par mode de calcul permet ensuite d’en vérifier les mesures dans une symbiose qui permet d’attester que la quadrature du cercle peut être tracée.Il est donc faut de penser que le carré d’un cercle ne puisse être dessiné à la règle et au compas, ces deux outils pouvant démontrer la quadrature d’une mesure multipliée par π. La vérification géométrique par le dessin des extêmes multiples de π permet de tracer une seule ligne de l’espace dont chaque extrêmités verticales déterminent deux droites parallèles entre elles passant aux abscisses des deux carrés dont les côtés sont multiples par π. Toutefois, l’irrationnalité de certaines mesures ne pouvant être triangulée, seule “une machine à remonter le temps” peut permettre l’ensemble des vérifications. Par la géométrie et nécessairement l’algèbre qui seule atteste l’intégrité du dessin.