At eight sides, a proportion of four to six,
Between the double lines two-tenths are contained.
(The next line) is at three times six from the double lines,
And the remainder is divided into three.
Le Lu ban jing est un manuel de construction destiné aux artisans, pour la réalisation de maisons, écuries, greniers et tombeaux, de valeur symbolique semblable à celle des maisons. L’outillage des artisans est souvent rudimentaire, et leurs pratiques des notions constructives soumises à la fréquence avec laquelle ils peuvent construire, suivant tel ou tel autre procédé mis en oeuvre dans la construction. Pour cela, leur formation est essentiellement orale et soumise à l’élémentaire qu’il est possible d’assimiler rapidement pour se souvenir de tous les éléments pratiques indispensables à leurs réalisations. Dans cette nature, le verset est essentiellement descriptif suivant un mode de représentation facile à retrouver par le dessin d’une esquisse, dont les éléments essentiels font seulement références aux notions de géométrie connus. Le vocabulaire est élémentaire afin de souligner par l’évidence les lignes principales qui aboutissent au dessin.
Toutefois, la difficulté réside en la manière dont il faut parvenir à penser la composition des quatre vers pour être en mesure d’imaginer la logique instruite à la compréhension des artisans. Nous avons de nos jours, règles, compas, équerres et raisonnements semble-t-il immuables pour tracer des perpendiculaires ou des parallèles suivant le vouloir, seulement mis à condition du savoir, mais tellement ancré que nous n’imaginons pas que les choses puissent être autrement conçues que par cette logique de l’outil au dessin. Pourtant, à l’époque où ce verset fut écrit, il semble que l’utilisation de l’equerre n’était pas courante, que la notion de mesure était encore variables, mais que l’unité savait être comptée.
Comme Vitruve sous l’antiquité exprimait les mesures en nombre de modules, le Bagua xian koujue parle d’unités entières ou de demi-longueurs, qui servent à la multiplication. L’artisan de l’époque semble connaître le tracé du cercle, et le report du rayon sur le périmètre pour le diviser en six segments égaux. L’auteur du verset connaît la géométrie et semble connaître les notions de calcul qui permettent de définir la valeur de l’unité par laquelle rediviser le cercle, non plus en six segments, mais en huit, et sans devoir mesurer les angles. C’est là sans doute qu’est toute la particularité du verset qui dessine le polyèdre par mesures de proportions dans lesquelles se dessine une autre forme d’équilibre que celle obtenue par la mesure du rayon.
Le titre du verset n’évoque rien qui soit relatif au cercle, mais le premier vers en résume la proportion et la division. La proportion est celle de “quatre par six”, qui correspond à la division du rayon reportée six fois sur le pourtour du cercle, mais aussi les quatre quarts de cercle dans lesquels sont comptées six unités, et la méthode de tracé des six segments d’un cercle sans qu’il soit nécessaire d’en dessiner le contour. La division est celle par laquelle le nombre des unités comptées devra permettre de trouver la mesure qui divise le cercle en huit segments égaux dont chaque quartier est la moitié d’un quart de cercle.

23- Tracé d’un héxagone par le dessin des parallèles aux axes du polygone.
La méthode du Bagua xian Koujue consiste à dessiner la règle par laquelle chaque mesure du rayon d’un cercle pourra être reportée, non pas suivant une unité de base, mais un diamètre pré-défini. Partant du coeur de l’arbre, une première ligne est tracée. Sur cette ligne sont contenus deux rayons du cercle voulu. Le cercle tracé régulièrement autour du centre, la longueur du rayon est reportée six fois. Chaque intersection obtenue sur un demi-cercle se projette symétriquement sur l’autre moitié et coupe l’axe du cercle par le milieu des deux rayons. Cette valeur constante, permet de vérifier le tracé et poursuivre le dessin.
Les quatre segments de l’axe sont à nouveau divisés par deux, ce qui permet d’obtenir huit unités sur la longueur du diamètre. Chacune de ces unités est à nouveau divisée par deux, ce qui permet d’obtenir huit unités, mais contenue cette fois dans la longueur du rayon. Ces huitièmes de rayon sont ce que le verset traduit par “tenth”, en tant que mesures de proportions constantes qui déterminent la plus petite longueur de la règle de calcul.

Les trois segments du premier demi-cercle sont alors divisés par la longueur de chacune de ces unités, ce qui permet d’obtenir huit unités par segment et quatre doublets. “Between the double lines, two tenth are contained” met l’accent sur la longueur réelle de chacun de ces segment, “two tenth“, par laquelle le dessin final devra diviser le polygone en longueurs égales qui puissent être comptées. Ainsi, “(The next line) is at three times six from the double lines, And the remainder is divided into three“, permet de marquer les intersections sur le cercle par lesquelles le nombre d’unités contenues permet d’obtenir la longueur de chaque huitième de cercle dans les directions recherchées.
La fraction de calcul ainsi développée est de trois quart la longueur du rayon, ce qui souligne toute l’estime que l’on peut avoir pour la compréhension du verset, sans doute courante dans les applications artisanales, mais certainement issue d’une longue réfléxion sur la manière d’élaborer le dessin d’un cercle, et l’ensemble de ses régulations.

Pour comprendre l’idée qui a dû prévaloir dans le tracé de ce dessin, nous devons rechercher la figure géométrique dans laquelle huit directions sont naturellement déterminées. Le seul polygone parfait est le carré dans lequel les diagonales marquent quatre directions et les axes passant par le milieu de chaque côté, quatre autres directions orthonormées. La longeur d’un demi-axe se reporte huit fois sur le périmètre du carré, le divisant en huit triangles isocèles égaux. Le cercle inscrit dans le carré dessiné à pour diamètre la longueur d’un côté, pour rayon la longueur du huitième de périmètre du carré et pour centre le point d’intersection des deux diagonales. De la même manière que le carré se divise en huit segments égaux, cette même valeur se reporte dans le cercle pour le diviser en six segments.
Pour dessiner les huit directions d’un carré dans le tracé d’un cercle, il faut donc parvenir à le diviser en huit segments égaux, non plus sur des lignes droites et perpendiculaires, mais sur une ligne courbe régulière et fermée. Pour cela, la définition de la règle de calcul consiste à déterminer le plus petit dénominateur commun aux divisions du cercle et du carré. Ce dénominateur est celui dont la fraction par huit et par six permet de trouver la mesure quantifiable dans la longueur du rayon, lorsque divisé en nombres pairs, chaque segment peut être redivisé en deux.

Nous savons pour cela que le rayon se reporte six fois sur le périmètre du cercle, que le demi rayon se reporte douze fois et le quart de rayon, vingt quatre fois. Dans cette division en vingt-quatre segments, trois est le dénominateur pour obtenir huit sections. Il suffit donc de refaire le chemin de la règle en comptant trois mesures là où il y en avait quatre pour que le cercle se divise huit fois au lieu de six. Trois mesures, sont trois “double-lines” ce qui donne six unités de la règle reportées sur chaque segment des huit divisions.
Le carré est une forme théorique de perfection des lignes parallèles et perpendiculaires, d’égale longueur, dont la composition permet d’obtenir une figure stable. S’il est facile d’en produire le dessin par le tracé de deux triangles dont la géométrie est indéformable, la nature du support ne permet pas la régularité avec laquelle il faut s’appliquer aux dessins de construction. Il est alors probable que le dessin des huit directions du cercle serve ici au tracé de coupe pour une colonne certe, mais également une poutre, une panne ou un poteau de section carré, rectangulaire ou octogonale , suivant la disposition des pièces de bois dans la construction.

Toutefois, il faut replacer le Bagua xian koujue dans son véritable contexte, car s’il peut sembler juste que le tracé décrit dans les quatre vers du verset permette de réaliser le dessin des huit directions d’un cercle, la géométrie reste cependant imparfaite, et de simple valeur élémentaire. Les quatre vers donnent seulement des indications qu’il appartient aux artisans de parfaire pour obtenir une figure équilibrée.
La division du rayon en quatre, puis huit unités permet de définir une proportion par laquelle trois quart de rayon coupent le cercle en chaque point des diagonales d’un carré. Mais le tracé géométrique reste imparfait si l’on ne considère que les unités du rayon. Il faut donc parfaire la forme énoncée dans le premier vers en applicant la méthode de division du rayon à celle qui permet de rediviser le cercle, par la moitié des portions de la courbe et succéssivement jusqu’à obtenir huit unités par sixième de quartier. Ainsi, chacune des valeurs reportées sur le cercle peut corriger la règle portée sur le rayon.

29- Dans un carré, le demi-cercle de diamètre l’un des côté coupe la diagonale en la huitième proportion un quart du cercle inscrit dans le carré.
“At eight sides, a proportion of four to six“, permet ainsi de définir par le compas, la position des deux axes orthonormés. Ceux-ci ont une proportion de quatre unités sur le rayon et six unités par quart de cercle réparties sur chaque segment de l’héxagone. Mais chacune de ces unités ne peut être reportée qu’avec approximation sur le cercle, à l’exception des quatre directions axées sur le centre.
La méthode la plus simple pour tracer les quatre autres directions consiste à diviser chaque quart de cercle en deux quartiers égaux par la mesure aux extrêmités des axes de la moitié des quatres segments. Le milieu reporté sur le cercle le coupe suivant des angles égaux, invariables et parfaitement reportés huit fois autour du centre.
Il faut donc voir dans le Bagua xian koujue, non pas une méthode de tracé rationelle, mais purement empirique et suffisament aléatoire pour éveiller toute l’intérrogation du sens que pouvait avoir ce verset dans ses différentes applications. Le repport des vingt-quatre segments suivant la divisions des côtés de l’héxagone ne résulte qu’en une figure irrégulière, trop imparfaite pour la construction. Et s’il est vrai que l’utilisation du tracé aurait pu servir au dessin de coupe pour une colonne, la nature de l’imprécision éveille cependant des doute sur la véritable importance du tracé dans la charpenterie.

Cependant, l’issue du verset précise comment le cercle doit être divisé en huit directions dont chaque segment comprend trois unités. Chacune de ces unités doivent être égales entre elles et diviser le cercle en un multiple des six segments de l’héxagone. Il est donc possible que la véritable nature du dessin évoqué consiste à déterminer la valeur réelle de chaque tier de direction qui ne peut être obtenue que par le dessin des lignes invariables des deux figures.
Lorsque l’on reporte sur le cercle la moitié des segments qui divise le cercle en quatre autres portions, on obtient la position exacte des diagonales d’un carré. Suivant le calcul du dénominateur commun aux six segments d’un cercle et aux huit d’un carré, on arrive à la logique qui détermine la vrai grandeur du tier des segments de l’octogone. Cette vrai grandeur est celle contenue entre le point de l’héxagone sur le cercle, et celui de chaque diagonale. Cette mesure reportée quatre fois entre chaque portion de cercle de l’héxagone, redivise parfaitement le cercle en vingt-quatre quartiers égaux.

32- Epure permettant de tracer le Bagua xian koujue. Sur le demi-cercle de gauche, les segments de l’hexagone sont divisés par moitié en quatre unités portées successivement sur le cercle. Chaque unité contient deux “dixièmes” dans la proportion de
(/12)/(1/8) = 2/3 fois plus grande que le huitième de rayon.
Sur le demi-cercle de droite, ces mêmes proportions qui divisent le demi-cercle en douze segments est contenue entre la projection du rayon sur le périmètre du cercle et la diagonale des deux axes. Ainsi, les douze segments peuvent être dessinés par report de la mesure sans qu’il soit nécessaire de diviser les segments de l’hexagone par chaques moitiés de longueurs portées sur le cercle.
En comptant trois fois une proportion de
Ces vingt-quatre quartiers fractionnés par mesures de trois divisent le cercle en huit portions, qui correspondent à celles de la géomancie chinoise dans le dessin du compas de construction. Le luojing ou luopan est probablement issu de l’enseignement de l’école de Jiangxi fondée par le maître Yang Yunsong durant la deuxième moitié du IXème siècle. Cet enseignement fût repris durant la première moitié du XIème siècle par l’Ecole de Fujian et transmise aux époques ultérieures du Lu Ban jing jusqu’aux réalisations les plus récentes.
Le dessin de la règle suivant les proportions du rayon puis celui du compas en huit et vingt-quatre segments se redivise en unités plus petites, qui portées au nombre de quinze, divisent le cercle en 360 degrés correspondant à une année de douze mois de trente jours. Si le dessin du luojing n’en traduit pas imédiatement l’évidence, nous en retrouvons pourtant la référence dans le Lu Ban jing pour déterminer la situation du ciel en chaque direction du compas. L’année commence au printemps par le premier tier Est du compas et se poursuit au Sud puis l’Ouest et le Nord jusqu’à former une année. Chaque tier des huit quartiers comprend quinze jours qui divisent l’année en huit cycles de quarante cinq jours. Ces jours sont également le nombre de degrés qui définissent chaque angle du cercle complet, soit 45° entre les rayons de chacune des huit directions.

Le dessin complet du compas chinois divisé en huit segments de trois unités nous permet ainsi de mesurer la valeur d’imprécision du dessin du Bagua xian koujue. Si l’on considère le cercle divisé en 360 degrés, le dessin de l’héxagone suppose que le nombre d’unités contenues dans un rayon est de 60. Cette mesure du rayon multipliée par deux et par π est supérieure de 16.99112 degrés. A l’inverse, lorsque l’on divise 360 degrés du périmètre du cercle par deux et par π, le nombre de degrés contenus dans le rayon est de 57.29578. Si l’on fait la fraction de 376.99112 par 360, on obtient un rapport d’imprécision de 1.0471976 unités entre la droite du rayon et la courbe du cercle. Ce rapport d’imprécition est la valeur de réduction d’un degré mesuré sur le cercle que l’on reporte sur le rayon, soit 1 divisé par π/3.
Inversement, cette imprécision détermine la différence de longueur entre les unités comptées sur l’héxagone et celles obtenues par projection sur le cercle. Si le rayon fait soixante unités, la portion de cercle contenue dans la longueur d’un segment de l’héxagone en mesure 62.831856. De même, si l’on considère la longueur des côtés de l’octogone elle sera de 47.123892 unités. Cette valeur divisée par le huitième de cercle, soit 45 degrés, nous donne une différence d’un rapport de 1.0471976. L’angle d’imprécision est de 2.123892 degrés.
34- Différentes mesures proportionnelles au rayon sont reportées sur le périmètre du cercle. La longueur du rayon divise un demi-cercle en trois segments, la moitié du rayon en six segments, le quart de rayon en 12 segments et le huitième en 25 segments. Cette dernière mesure, supérieure à la logique, introduit la notion de , supérieure à 3 et par laquelle la valeur du rayon peut être multipliée pour exprimer la longueur d’un demi-périmètre de cercle.
L’imprécision du Bagua xian koujue est inscrite dans la valeur de π, variable elle aussi suivant le nombre de divisions portées sur le cercle. Si la géométrie vérifie le dessin par la démonstration de valeurs mathématiques, l’objet d’un tracé de construction est d’en réduire l’imprécision par le simple procédé de la juste mesure portée. Cette mesure n’a de rigueur que dans l’esprit de l’artisan lorsqu’un défaut de proportion incite à définir autrement les mesures. Et celles-ci pour être trouvées, doivent d’abord être dessinées.
Le développement précédent a permis de démontrer comment les quatres lignes prenaient figure de géométrie, pour dessiner une lecture simple, mais imparfaite, en laquelle toutes les résolutions peuvent établir les mesures. Ces mesures sont des proportions portées du rayon sur le cercle, non pas en tant qu’unité de longueur mais de fraction d’une unité donnée. Celle-ci, divisée par deux, et successivement jusqu’à la plus petite longueur sert de schéma linéaire aux applications de division d’une courbe. Le geste de division d’une droite, que tous les artisans connaissent peut réguler la division d’une courbe pour obtenir un polygone régulier.

La valeur mathématique est exprimée dans le cercle sans qu’il soit nécessaire de définir une valeur de π, mais si le dessin est de rigueur vérifiable par ajustements, toutes les compositions restent cependant restrictives. L’octogone dessiné par la méthode du Bagua xian koujue ne permet pas de dessiner le polygone régulier dont la longueur du côté est la mesure connue pour construire le dessin du cercle exinscrit sur lequel reporter chacune de ces mesures.
Une méthode élémentaire enseignée dans nos écoles consiste à dessiner l’un des côtés de l’octogone, l’axe médian et le demi-cercle de diamètre le côté. Le demi-cercle coupe l’axe en un point qui est le centre du cercle dans lequel le dessin de l’octone est inscrit. Pour terminer le dessin, il suffit de reporter huit fois la longueur du segment sur tout le périmètre du cercle. Chaque mesure des côtés de l’octogone est unitaire et facilement quantifiable par des multiples de deux, mais ce que les mathématiques permettent, la géométrie ne sait le faire lorsqu’il s’agit de diviser la longueur du segment en trois.

37- Dessin de l’octogone
Une autre méthode de géométrie appliquée consiste à dessiner le Bagua xian koujue à l’envers. Connaissant la longueur d’un segment, le dessin consiste à chercher le cercle sur lequel reporter vingt-quatre fois la mesure donnée. Ce dessin, loin des qualités artisanes de la logique immédiate, implique deux étapes de la mise en oeuvre, l’une étant dessinée, l’autre construite. Et c’est là sans doute que commence l’histoire de l’expression des formes géométriques.
L’écriture est un dessin qui implique le langage. Le dessin est un langage qui implique l’écriture. La transmission de connaissances nécessite les deux sens de la vue et de l’ouïe pour permettre à l’esprit d’ordonner la pensée suivant deux pôles de réception qui vont de l’esprit à la main et de la parole à l’oreille. Pour cela, les mathématiques ont inventé une expression des nombres pour en connaître à la fois les mesures et les proportions, et nous pouvons, dans ce langage exprimer une géométrie.

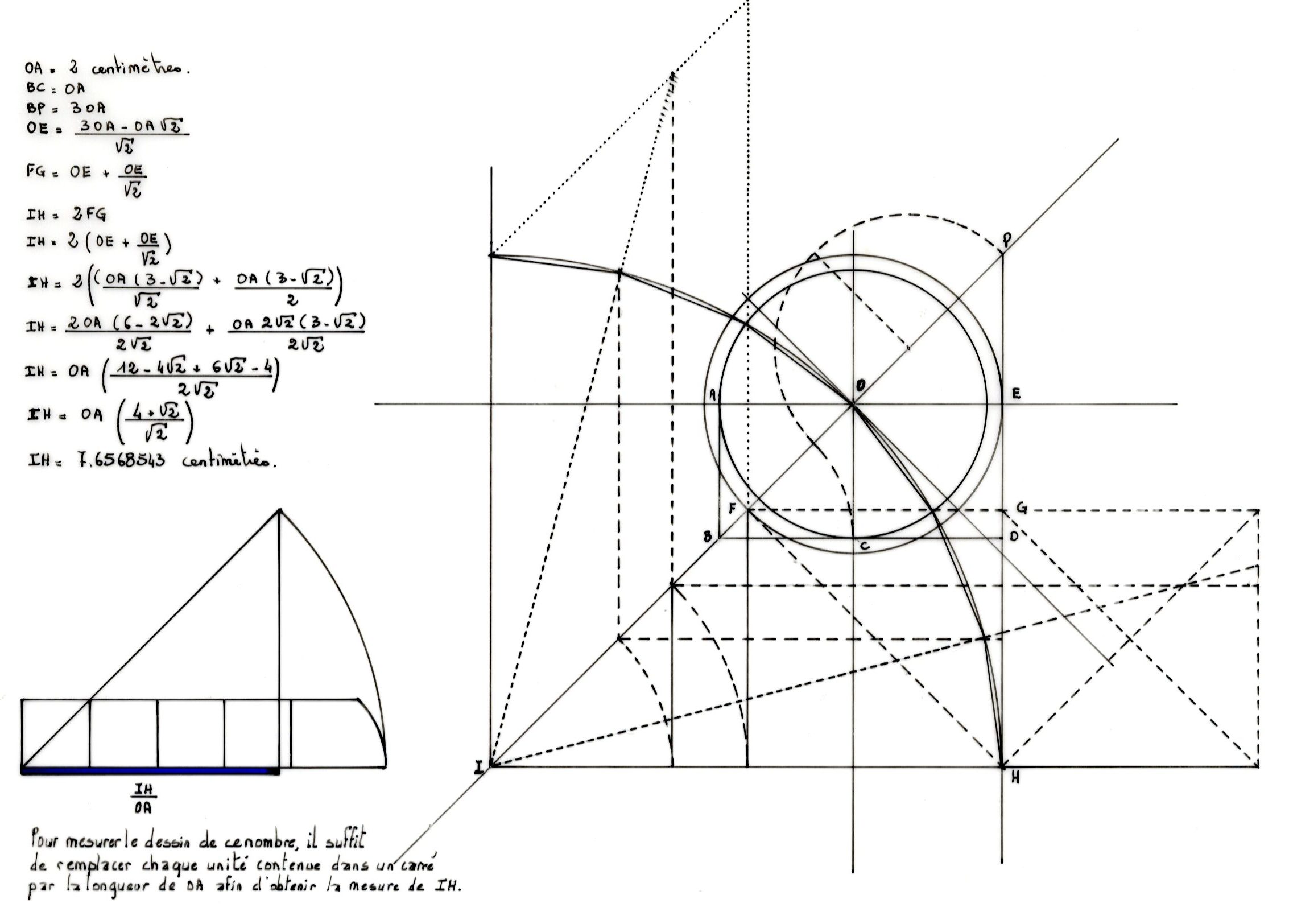
38- A gauche, dessin du Bagua xian koujue, lorsque l’on fait le cheminement inverse pour dessiner un octogone dont on connait l’une des longueur de ses vingt-quatre divisions. On commence par tracer le cercle de rayon l’un des vingt-quatre segments qui divisent le cercle cherché, puis les deux axes orthonormés et les deux médianes. On trace ensuite un carré ABCO dont le côté est la longueur du rayon. Du sommet B de ce carré, on reporte trois fois le rayon du cercle sur la diagonale passant par O. La longueur BP ainsi obtenue forme un triangle isocèle BPD coupant l’axe horizontal du premier cercle en un point E. La longueur OE est le rayon d’un deuxième cercle coupant le segment BP en un point F. La projection de F sur la droite PE coupe perpendiculairement cette droite en G. La longueur FG est la moitié du rayon du cercle cherché et FP la moitié de longueur de la diagonale. Pour trouver le centre du cercle, il suffit de tracer le cercle de rayon FP qui coupe la droite BP en I et la droite PD en H. IH est deux fois la longueur de FG et OA est (IH2)/(4+2) fois l’unité de longueur. FG est (OE(1+2)/2) et OE = (3OA-OA2)/2.
Si l’on calcule la valeur de dans le dessin du Bagua xian koujue avec un cercle de rayon 1, on obtient une valeur de
=3,1323286. Cette valeur divisée à 24 OA donne IH = 7,6612976. Dans le dessin de cette géométrie de l’octogone, =3,1344465.

Cette géométrie du langage exprimée dans la ligne de courbes et de carrées est un idéogramme, bien différent de ceux exprimés en quatre vers. Le dessin recherché dans l’expression des lignes est identique, mais le déroulement, différemment composé. Cela implique un raisonnement “atomique” de la matière dessinée qui dans le Bagua xian koujue passa par l’oral bien avant de trouver verset. Dans l’idéogramme ici composé, le langage est mathématique, sans valeur autre que l’expression du nombre pour traduire de pratiques liées à la construction. Hors, la construction est la maturation essentielle qui précède le nombre avant que des valeurs distinctes ne soient fixées.
Dans le Bagua xian koujue, la division par huit est seulement évoquée par le titre du verset, mais certainement d’évidence à pouvoir conduire le raisonnement conçu dans l’esprit initié des artisans. Ce nombre de division d’une mesure en huit segments égaux est règle courante dans la construction et certainement par habitude de l’usage de proportions en huitièmes de mesures.



Les jours comptés de quinze en quinze, et les années en vingt-quatre quinzaines déterminent dans le temps, toute l’ampleur du nombre. Huit est une division non seulement coutumière de la Chine mais également des mathématiques modernes qui dans le dessin des formes simples, établit des rapports de proportions. Ces proportions, pour devenir essentielles à la nature des connaissances de l’homme, trouvent toujours un sens dans l’expression qui puisse retenir par l’évidence, la mystique éclosion de l’emmerveillement.
La géométrie est source d’emmerveillements et le nombre en exprime ailleurs la familiarité dans l’évidente logique qui semble parvenir chaque fois que le nombre est sujet du rêve porté en chacun d’être fondé dans ce milieu. Un milieu de nature où tout s’énumère dans l’ordre d’une création, pure et simplement fondée sur la valeur concrète des entiers, matériaux de la vue qui composent l’infini de toutes les valeurs cachées.

45- Ces proportions sont de 2 du carré à l’octogone, 4/ du carré au cercle, 4/(2) du cercle à l’octogone, /2 du cercle au carré et 2 d’une forme géométrique à sont homothétie. Si le rayon = 1, l’aire du cercle est 6,2831853, celle du carré mesurant 2 de côté est (2) x (4/) = 8, celle de l’octogone 8/2 = 5.6568543. Cette mesure divisée par 4/(2) = 6,2831853 puis par /2, on obtient l’aire du carré inscrit = 4. L’aire du carré inscrit divisée par 2 donne l’aire de l’octogone inférieur = 2,8284271 divisée par
4/(2) = 3,1415927 puis par /2 = 2.
Le Bagua xian koujue dessine le temps, les points par où le soleil passe, et ceux par où il est caché. Cette mystique appliquée au nombre fut élaborée par l’emmerveillement que le nombre en lui-même su invoquer pour retenir l’attention du Levant. Ailleurs, l’invocation de l’élément figuré par la géométrie fit recherche de toutes les manières d’élaborer le dessin, pour sa nature implicitement mystique de la constance des nombres entre eux.
Cette constance, si parfaitement saisie par le langage mathématique en valeurs exprimables dans la nature des proportions, traduit une hiérarchie spatiale des formes de la nature, non pas organisées suivant un hazard de conception humaine, mais une logique qui conduit d’une une ligne à une autre dans la relativité des proportions. Ces proportions si naturelles ne sont dessinées que par le cercle qui va de l’octogone au carré, et ainsi d’une forme terrestre à celle d’un monde construit.
Lorsque par d’autres polygones le cercle révèle toutes ses ressources, l’emmerveillement est seule constante exprimable par les nombres, si intimement imbriqués à la vie qui nous éveille que l’architecture s’inscrit dans cette immortalité. La splendeur mise au jour est matière d’élévation d’une âme simplement vêtue de l’oeuvre fascinante que le cercle enumère en l’épure d’un seul trait dont la ligne dessinée n’a de commencement ni de fin.
Les polygones inscrits dans le trait d’un cercle sont les seules figures qui fractionnent la ligne comme la neige en cristaux défait les particules rayonnantes dans le cercle d’une goutte d’eau. Le corps de la vie est ainsi composé de l’imbrication des formes entres elles, jusqu’à concevoir l’équilibre terrestre par lequel la chair est animée. La vie, est cette nature génitrice de toutes les géométries du cercle dans lequel l’éclosion étire la ligne pure en autant de figures qu’il y a de matrices pour imbriquer entre eux les gênes constructeurs.
Des racines des nombres à celles qui font croître les matières vivantes, l’emmerveillement du géomètre est indistinct de cette géographie où la sphère, reflet de l’iris, est unique en sa diversité. Tout paraît dans l’aspect des formes et apparaît dans le dessin lorsqu’une fascination arrête un point d’observation sur la nature des formes. Elles deviennent moins parfaites, incontrolables à l’entendement lorsque tout d’évidence simple se montre de complexités composées. Jusqu’à la raison qui impose des lois dans le dessin des géométries pour parfaire les lignes et mesurer la pureté de l’édification naturellement conçue.
La pureté si essentielle est pourtant comme un coeur vivant, parfait dans le pouls qui tend ou relache le muscle, car de chaque phase de cette vibration, s’affirment toutes véritées de la vie continuellement identiques à l’universalité des lois. Le flux de l’essence terrestre traverse tous les corps, par le souffle d’une voie céleste qui anime le ciel lacté, en cette profusion nébuleuse de petites lumières intérieures qui ramènent à la question de la vie dans son mouvement.
La géométrie, caprice de l’évolution humaine, est une source de vitalité essentiellement constructrice d’invisibles qui accomplissent l’union de l’homme à son environnement terrestre. Sans la raison de cette vie là, géométrie intime du géographe, rien de ce qui porte vie ne reste à l’entendement de comprendre pourquoi la valeur des nombres est d’importance à faire Sciences de fondements liés à la terre, comme l’instinct à l’inconscient.
L’arbre par ses racines est lié à ce qui compose la terre, et de son bois se fondent les charpentes de maisons. Cette harmonie indistincte est source de légendes en lesquelles l’architecture construit la géométrie. Une géométrie régulée par le sens des éléments que chaque corps géométrique inspire au concepteur. Le cercle et le carré ont fait voûtes et places fortes pour édifier l’environnement au-delà des beautés naturelles, par celles quelque fois, mûries en l’esprit habile des rêveurs de l’humanité qui ont fait Sciences de la pensée.
Charpentée en théorèmes et démontrée par le nombre, la géométrie est devenue une science de l’espace non plus sarmenteux des inventions de jadis, mais surtout talonné de découvertes nouvelles. Elément de fondation de toutes les mathématiques, la géométrie disparaît dans la mesure du nombre devenu irrationnel par force d’équations succédant à toutes celles déjà trop dépassées. 1 n’a plus de sens dans la mesure du mètre et plus de mystères n’aiguillent les questionnements vers la logique de l’homme dans le fondement d’une géométrie d’où la canne du maître tire les mesures.
La connaissance a besoin d’emmerveillements successifs pour renouveller le précepte de l’édification, qui de l’être balbutiant les premiers vers d’un alphabet en vient à connaître de coeur toutes ses tables. Mais elle est dans la vie comme un pouls capiteux dont il faut clarifier l’esprit monade pour extraîre le fruit de la fondation qui conduit l’élévation jusqu’au sommet. L’ultime est dans la recevabilité de l’instinct par le corps imprégné de ce fruit que la connaissance a pressé des éléments du savoir jusqu’à faire dans l’homme une différence de nature. La géométrie merveilleuse des connaissances vitales est celle élevée dans l’instinct de traduire par les formes ce qu’elles évoquent de vital à toute l’évolution du corps de l’humanité.
Quatre lignes d’un verset ont porté connaissances sur le cercle, moins peut-être pour créer que connaître la structure de l’élément simplifié dont chaque ligne se compose de nombres. Ces nombres ont bercé les esprits les plus anciens et de l’Antique nous gardons cette secrète indulgeance du géomètre sur le moderne qui dans la limite arrêtée, fixe des mesures que seul l’espace confronte. L’artisan du tracé des lignes d’une charpente connaît par les sens la vérité des nombres, et s’il vient à succomber au mystère décimal, ce n’est que par respect des beautés qu’il connaît.
Les théories mathématiques sont une praxis des géomètres, dont l’enthousiasme poétique a du créer un nouveau langage, plus rationnel que l’unité et de logique applicable, mais dans le cercle seulement des praticiens de cet idiome. Le langage est raison d’être avant d’être une connaissance, et ce fruit ne mûrit qu’à force d’années à démontrer la raison d’exprimer par mesures la valeur des entités qui composent l’univers proche de cette commodité.
Il résulte de l’étude du Bagua xian koujue un sentiment de pouvoir redire les formes telles que connues par les nombres qu’énumèrent les Sciences, mais sans devoir en créer de nouveaux. De là, une longue poétique de l’imaginaire inscrite à la suite du Bagua xian koujue pour tenter de placer à notre époque l’importante géométrie qui nous compose. Cette géométrie de l’environnement est de nature impliquée dans la composition dont l’imaginaire se transforme pour inspirer le fondement d’une relation entre les formes telle à pouvoir concevoir dans la forme le dessin des régulations.
L’octogone issu d’un carré n’a d’autre sens que la géométrie sans doute trop terne pour éveiller l’harmonie qui inspire le cercle. En diviser les segments par le rythme d’une mesure comptée ramène au sens secret de la forme dans son entier, si fécond d’un univers où le cercle tourne par années autour d’un point dont le soleil régule chaque journée. Passant par une fenêtre, le soleil dessine un centre d’où s’élèvent toutes pensées naissantes en la matière que l’architecte compose, pierre après pierre en d’autres mains, pour élever l’esprit des formes dans le vécu des quotidiens. L’octogone dans un cercle fait quadrature du ciel entier, pour rappeler à chaque jour, la vie par sa beauté.

EPURES